Back to start site

A Twice Double Acting a  - Type Stirling Engine Able to Work with Compound Fluids Using
Heat Energy of Low to Medium Temperatures.

Note: Some greek letters may not appear in the right way. This HTML-page is tested with Netscape 4.06 Browser and MS Internet Explorer 4

Contents

Preface

Development Potential of the Stirling Engine

Heat transmission

Working Principle

Sealing

Power Control

The thermal efficiency htherm

The Load Exploitation Factor  e i

The Cyclic Torque

T - S Diagrams

Conclusion

Stirling engine drives Stirling refrigerator

Literature

Abstract:

It is one of the most important challenges of our time converting solar energy to electricity or mechanical power. One possibility of doing this is shown here by a new construction of one of the world eldest engines the "Stirling Engine" .

This report gives some details of the operating- and construction principles, and some figures to illustrate the engine and the computer simulation results.

This Stirling Engine with 8 cylinders is twice double acting. Its special highlight is the facility for the heat transfer from a liquid to the working fluid which results in extremly low temperature losses. The engine is able to work with compound fluids. Some more   Highlights are the high space ratio of Vmax / Vmin > 4.5 and the engines power control which is really simple and fast working by changing the deadspace in the cylinders.

Because of the nearly isothermalized heat transfer the efficiency is near carnot's, that leads to the possibility to take simple solar-collectors for the heatsource. A solar-thermal power plant with such collectors may be cheaper than a plant with sunshine-following mirror systems, although these -more expensive- mirror-collectors will produce higher temperatures.

Sealing problems are reduced: Not the pressurized working gas but the pressurized working liquid is to be sealed against the atmosphere.

A disadvantage is the engines slow rotation, which can be compared with large diesel ship-engines. But that is not at any case a disadvantage because the energy transfer is a function of time.

This 4 times (= 2 times double-) acting Stirling engine is able to work as a room refrigerator. By this the one double acting Stirling engine drives the other double acting machine which is switched to a refrigerator. See the chapter Stirling engine drives Stirling refrigerator .

2 of these Stirling engines coupled on one crank-shaft by a difference of 135 degrees will have a constant torque like a steam turbine. Manufacturing this new Stirling Engine is simple. The engine can be used to work in solar thermal electric power plants, or to drive pumps, even for driving ships.

A first Prototype of this engine has been tested.

All calculations, tables and figures in this report are done with the computer program STMOT2:

press Your browsers Return button to return into previous text

  Back to contents

To make solar energy worldwide accessible in such way, as to supply us with electric and mechanical energy and to make solar energy suitable for storage and transport are the greatest challenges of our time. This does not only apply to science and technology, but in the same amount to economic and environmental policies. The use of hydrogen in the powerproducing industry is an answer to this challenge, which can be realized |1|,|2|. Current for the electrolytic hydrogen production can best be produced in solar thermal power plants. If required, solar thermal power plants can also produce current from conventionally generated heat. Parabolic mirror trough collector power plants -driven solely by solar energy- already reached current producing costs of 0.16 $/KWh see |5|,|6|. On the current producing side, these plants consist of conventional plant construction with a Rankine thermal power process on water vapor turbines. These plants have been in use for several years. They are the most cost effective solar generators, which have been built and put to use so far. However, the steam turbine is a weak point in these plants, as far as efficiency is concerned. The steam produced by solar energy is at 100 bar at 371 degrees C. This temperature is too low for a good thermal efficiency of the steam turbine, and/or the plant becomes more complicated and more expensive, if several intermediate heatexchangers have to be employed for better utilization of this state of steam .

In solar thermal power plants, a Stirling engine is, based on its working principle, probably the only thermal power engine, that can operate cost effectively and with a better efficiency at a lower temperature level than steam turbines will do. It should be developed to achieve greater economic efficiency. From another financial aspect too, solar thermal power plants, using a Stirling engine, should especially be developed for the use of low up to medium temperature heat sources (100 - 250 degrees C), because these engines could receive their energy from simple solar collectors, and not necessarily from far more expensive parabolic mirror trough collectors, which have to be readjusted in accordance with the position of the sun.

The photovoltaic current generation is sensible only for smaller units, from the point of view of justifiable current production costs, but it will be well suitable to cover special cases, which cannot be done by thermal power plants.

press Your browsers Return button to return into previous text

  Back to contents

An important development potential of the Stirling engine is the heat transmission to the working gas. Upon heat supply during expansion and heat reduction during compression, an optimally sized heat transmission surface within the engines working space should be in contact with the working fluid. It should grow with the expansion space and should renew itsself constantly in the compression space. With these options the engines "dead space" is almost reduced to the regenerator space only. By that the space ratio Vmax / Vmin can significantly be raised.

Another option to be wished for, already described by G.Walker |7|, which could however not be realized in real Stirling engines of high power hitherto, is a pressure increase caused by a compound working fluid. Thereby the steam partial pressure of a liquid caused by liquid-evaporating in the expansion cylinder is added to the gas pressure. This results in more work output per revolution, although the overall efficiency is reduced, -due to evaporating the liquid and condensing the vapor- as it could be seen, when interpreting the "frames" in   Fig. 4a and in   Fig. 4b. See chapter The thermal efficiency htherm

press Your browsers Return button to return into previous text

  Back to contents

The machine described -   Fig. 1 - constists of 8 cylinders, which, connected in pairs in U-pipe arrangement, act on 2 crank gears. A power transmitting piston is installed in the straight section of each of the 4 U-pipes, surrounded on both sides by a working liquid, which reaches into the cylinders. -More detailed description of the arrangement see development of the engine.- on this homepage.- This liquid is heated or cooled, but the actual heat exchangers for heating and cooling it are positioned outside the engine. A pressurized gas cushion, the working gas, is situated above the liquid. This gas now is heated or cooled within the respective cylinders by way of the liquid. Depending on the choice of temperatures in the expansion cylinder and a suitable working liquid, the resulting steam pressure of this liquid can under certain circumstances greatly increase the total pressure; so there is a compound working fluid acting in the engine. Evaporating the liquid has one more valuable effect. It performs an optimal heattransmission to the gas with a very small temperature gradient. This is optained by the very fast movement of the vapor molecules which are mixing together with the gas molecules. But also the disadvantage of compound fluid must be taken into account: It reduces the thermal efficiency by the condensing phase in the compression cylinder. We will discuss it later on by interpreting the "frames"   Fig. 4a and in   Fig. 4b. See chapter The thermal efficiency htherm

2 variants for the transmission of energy from the liquid to the gas shall be presented here:

1) Overhead irrigation of the gas with the working liquid via injection nozzles in the head section of each cylinder. This type of heat transmission to a gas recreates the weather reactions in our atmosphere. In this case, one pump each is required per cylinder, which sucks the liquid from the lower part of the cylinder, guides it via external heat exchangers -solar collectors and coolers-, and then returns it back into the cylinders by the injection nozzles.

2) Installations for heat transmission for heating and cooling the working gas in the gas space of the respective cylinder: The liquid in front of and behind the piston is pressed by the piston movement first through heat exchanger coils within the cylinders and then, in the gas volume moistens these installations, which may e.g. be spirally wound up wire mesh nets or metal chips. The heat exchanger coils within the cylinders as well as the walls of the cylinders are passed by a second liquid, which is heated or cooled in external heat exchangers, and is not influenced by the gas pressure within the cylinders see   Fig. 6.

In both variants for heat transmission, which can also be combined with each other in parts, a large heat transmission surface is available for the gas directly in the working cylinders. This surface grows with expansion and constantly regenerates itsself during compression, when the gas is irrigated, so that heat transmissions with low temperature loss can be achieved here. To give an idea, the installations for heat transmission are not included in   Fig. 1. The second variant is sketched in   Fig. 6. Fig. 1 shall only illustrate the working method of this twice double acting Stirling engine.

press Your browsers Return button to return into previous text

  Back to contents

In Stirling engines, the working gas is periodically moved between the hot expansion space and the cold compression space. In an ideal Stirling engine this movement takes place discontinuously. Its working process -see the P-V diagram   Fig. 2 or the T-S diagram   Fig. 4a - is equivalent to 4 changes of state, which follow after another in the ideal engine: isothermal compression from (I) to (II); isochoric heat supply from (II) to (III); isothermal expansion from (III) to (IV); and isochoric heat dissipation from (IV) to (I); see |3|. Along the isochoric changes of state at Vmax and Vmin no expansion work is done; during Vmin however a substantial energy supply is required and a heat absorption is required during Vmax. These amounts of energy are equivalent to each other. They should therefore remain in the process. A regenerator makes it possible to exchange them against each other internally.

In a real engine the isochoric gas exchange processes cannot take place instantaneously. For the inertia forces would be too strong, the changes of state must overlap. Usualy the succession of the changes of state is aproximated within a 2 cylinder engine by the way, that its pistons continuously move phase shifted to each other.

You may ask Yourself if You have seen   Fig. 1 how is this complicated engine come from? Detailed description of the development of this engine You will find at the site development of the engine.- on this homepage.

press Your browsers Return button to return into previous text

  Back to contents of report

The sealing of the working gas is less problematic in this engine. Only 4 piston rod gaskets are required in this 8 cylinder engine as sealing against the surrounding atmosphere. And these gaskets are no complicated gas gaskets but piston rod gaskets for pressurized liquids, as well known from hydraulics.

It is possible to have a hermetically sealed engine without mechanical crank gears if this engine is only for generating electric energy. (Have a look to the German patent No. DE 38 15 606) This engine is just the same as it is sketched in   Fig. 1 but the mechanical crank gears are substituted by two electromotive "crank gears" within the engine. This is a combination of an electric linear generator and a linear motor which is situated close to the piston in the horizontal area of the U-pipe. One of these combinations works between the cold cylinders K1-K2 and the other combination works between the cold cylinders K3-K4. In connection with an electric pistonway control unit the 90 degree phase shift is kept and the compression works are done by the motors of these two combinations. Expansion work results in electric energy through the linear generators.

press Your browsers Return button to return into previous text

  Back to contents

Power control of the common Stirling engines is performed e. g. by change of the gas load by pressure-reduction or pressure-increase via a gas resevoir and a compressor. A load regulation can be realized far easier in the engine presented here, by changing the "dead space" . For power reduction the liquid at left and right of the pistons is partly sucked into control cylinders "RC". (Sketched in   Fig. 1 below cylinders K3-K4, better to be seen as cylinders RC4 and RC3 in   Fig. 6.) By this the mass of the working fluid, which is transferred during the process between the hot and cold spaces, can be reduced. Some part more of the fluid then always remains in the respective working cylinder also during the upper dead center position of the piston and this part of fluid no longer takes part in the energy exchange. The fluids pressure is reduced at the same time. For fast power increase, the liquid from the control cylinders "RC" is to be returned into the U-pipe. A control volume of 25% each of the piston stroke volume leads to the inner graph which is the partial load see   Fig. 4a or the smaller graph in   Fig. 2.

Fast power control could also be achieved through temperature change, if the heat transmission to the working gas is achieved by irrigation with hot working liquid; in this case the irrigation stream can be reduced and/or mixed with colder liquid.

press Your browsers Return button to return into previous text

  Back to contents

The thermal efficiency htherm in case of isothermal heat transmission (TE in the H- and TC in the K-cylinders are constant) and at 100% heat exchange in the regenerator is equivalent to the Carnot efficiency:

hthermC = (TE - TC) / TE

This ideal thermal efficiency naturally cannot be achieved within the real engine. The heat transmission may be good, but is just only nearly isothermal. Temperature losses can be calculated from the heat capacities of the irrigation liquid drops (and/or that of the metal chips) and from the thermal capacity of the gas. They have been proved in experiments by the author.

During the heat transmission to the gas, size and mass of the heat exchange surface, gas velocity on this surface, thermal conductivity of the gas as well as the regenerator's quality   |9| are of influence for the thermal efficiency. Further the thermal -and the overall- efficiency is reduced with increasing rotation by friction losses in the liquids flow and by acceleration of the liquid masses. These mechanical losses and the temperature losses at heat transmission are kept low at slow rotation. Therefore, if a high overall efficiency is wanted, the engine is to be driven at slow rotations. Like the large diesel engines for ships, high power is attainable for this stirling engine by a large construction and high gas pressure.

If a compound fluid -gas + vapor- is chosen, the increase of pressure |10| by the steam partial pressure of the evaporating working liquid leads to more work output. Evaporating of liquid has the valuable effect, that it performs an optimal heattransmission to the gas with a very small temperature gradient. This is obtained by the very fast movement of the vapor molecules which are mixing together with the gas molecules. But also the disadvantage of compound fluid must be taken into account: It reduces the thermal efficiency within the condensing phase in the compression cylinder. The reason therefore is, that the amount of condensing energy is taken out of the process. At each cycle it must be produced new. This is well to be seen, when comparing the "frames" in   Fig. 4a and in   Fig. 4c which in both cases represent ideal stirling processes.

• Fig. 4a -with gas only- leads to the carnot-efficiency. The mass of working fluid is always constant.
• in -Fig. 4c- the "frame" is the theoretical ideal stirling process for the vapor component as the only working fluid. You see this frame is not even nearly a parallelogram as is the frame in Fig. 4a. At the isochoric cooling phase at Vmax the mass of vapor is condensed to liquid until an equilibrium is reached for saturated vapor at temperature TC. Only a small rest of vapor is left. The mass of this small amount of vapor is compressed at temperature TC to Vmin. Now new vapor will be produced during the isochoric heating phase and the isothermal expansion phase. The energy needed for the isochoric phase cannot be a regenerator supplied energy. Only the small amount of vapor left during cooling and compressing theoretically can be heated by regenerator energy. The previous condensed liquid must be removed into the expansion cylinders liquid volume; here it is heated and evaporated again. This is the reason for the reduced thermal efficiency of an engine working with compound fluids.

Let us state: When using a compound fluid -gas + vapor- the work done per cycle is increased but this is done by reduced thermal efficiency.

But inspite of the reduction in thermal efficiency, compound fluid is valuable, whenever the cost for heatgenerating is neglectable, as it is with solar collectors or from waste heat.

press Your browsers Return button to return into previous text

  Back to contents

Apart from the thermal efficiency, the load exploitation factor -sometimes called the "Schmidt Facttor" - " n " is an interesting parameter. "n" is the relation of the engine's effective work "W" to the effective work of the ideal Stirling process " Wi " , in the same working space between Vmax and Vmin and the same temperatures "TE" and "TC" , but with a regenerator volume of VR = 0. "W" is equivalent to the areas enclosed by the graphs in   Fig. 2,   Fig. 3 or in   Fig. 4a.

The ideal Stirling effective work " Wi " , is equivalent to the area in   Fig. 2 represented by: (I) - (II) - (III) - (IV) - (I); or to the frame in   Fig. 4a, both areas are created by the isotherms TE and TC, as well as the isochores at Vmax and Vmin.

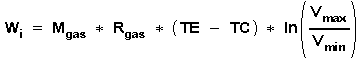
or

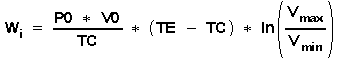
With Mgas = Mass of gas, Rgas = Gasconstant. V0 = expansion- + compression space, P0 = pressure, both measured in idle position.

The effective work output "Wi" of the ideal Stirling process in accordance with these equations is determined by the temperatures TE and TC, as well as by the volume ratio Vmax / Vmin that can be achieved, and it is directly proportional to the gas mass in the engine, which is determined by the idle volume V0 and the idle pressure P0. Principally the same applies also to the effective work "W" of the real engine. The volume ratio Vmax / Vmin is determined by control volume and other deadspaces, regenerator volume "VR" , the phase shift angle d and the geometric conditions of the crank gear movement, which can only aproximate the ideal movement. Vmax / Vmin and thus "W" and the degree of exploitation "n" are reduced at increasing "VR" and other deadspaces. Vmax / Vmin is also reduced, if instead of the purely sinusoidally movement of the pistons through the crank slot gears, connecting rod crank gears are used for "KU1" and "KU2". See the summary in table 1

The above mentioned load exploitation factor "n" is only usefull for comparing the work "W" of a real engine to the work "Wi" to its own ideal process within the same space range of Vmax and Vmin.

It would be more helpfull, if we can compare the work "W" of any real engine to the work "Wi " of an ideal stirling process of a common usable ideal standard reference stirling engine. With this new basis of " Wi " -now better named: " Wir " we should define a new load exploitation factor: " e i " The following proposal may be discussed for the definition of a common usable ideal reference stirling engine, and for the conditions of its process calculation:

• The ideal work "Wir " of the reference engine should be calculated with the equation above.
TE is the maximum temperature, which can be measured on the surface of the real engines heater -if the engine is heated by a burner or by radiation- or, if heated by a liquid, TE is the liquids temperature at the entry to the engines heatexchanger.
TC is the minimum temperature within the engines cooler. That is the temperature of the coolant at its entry into the cooler for the engines working fluid. Or TC is the minimum temperature of the coolers surface if the engine is cooled by radiation.
The mass of the working fluid is the mass of the gas which is constant within the real engines spaces including all dead spaces. If compound fluids are used, only the mass of the gas component should be taken, otherwise the above formula cannot be applied.
The space ratio Vmax / Vmin must be a constant standard value. Here we must set statements, otherwise there is no possibility to have a common usable standard for a reference process. There may be other definitions to define a constant space ratio, but

I prefer the following:

1. Going out from a 2 cylinder - 2 piston a type engine, both cylinders are of equal dimensions.
2. Ideal regenerator, but with regenerator space = 0.
3. No further deadspace. Heating and cooling the working fluid occur within the expansion- resp. within the compression cylinder.
4. If in a 2 cylinder - 2 piston stirling engine with a pure sinusodial crank gear, a shift angle between expansion and compression movement is d = -90 degree, then the minimum space Vmin is at the crank angle position j = 45 degrees and the maximum space Vmax is at the crank angle position of j = 225 degrees. This would lead to a space ratio -if no other deadspaces are to be taken into account- of:

   

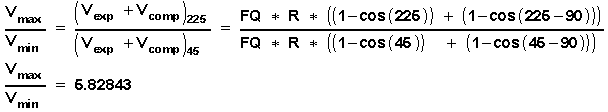
   This space ratio shall be the space ratio for the ideal reference stirling engine too.

• With these definitions: Temperature TE = Tmax and TC = Tmin and the constant space ratio Vmax / Vmin = 5.82843 the work of the ideal stirling reference process "Wir " is calculated according to the above formula for "Wi " to:

  

  

  
  

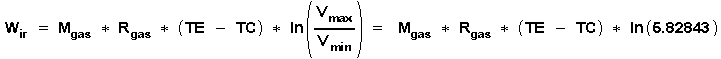
Now the load exploitation factor is " e i " , and no longer "n" .

or

"e i " is now of common validity. Its use says:

"How is the measured work "W" per revolution of my stirling engine with a given gasload of Mgas -represented by P0, V0 and T0- and with the given temperatures TE = Tmax and TC = Tmin in comparision to the work "Wir " of an ideal reference stirling process for the same temperature range and the same gasload."

If the rotation of the engine is taken into account, we now have the possibility to compare quality and real power of all stirling engines to a common usable ideal reference stirling engine.

A summary in table 1 illustrates the influence of the above mentioned parameters on "W" .

press Your browsers Return button to return into previous text

  Back to contents

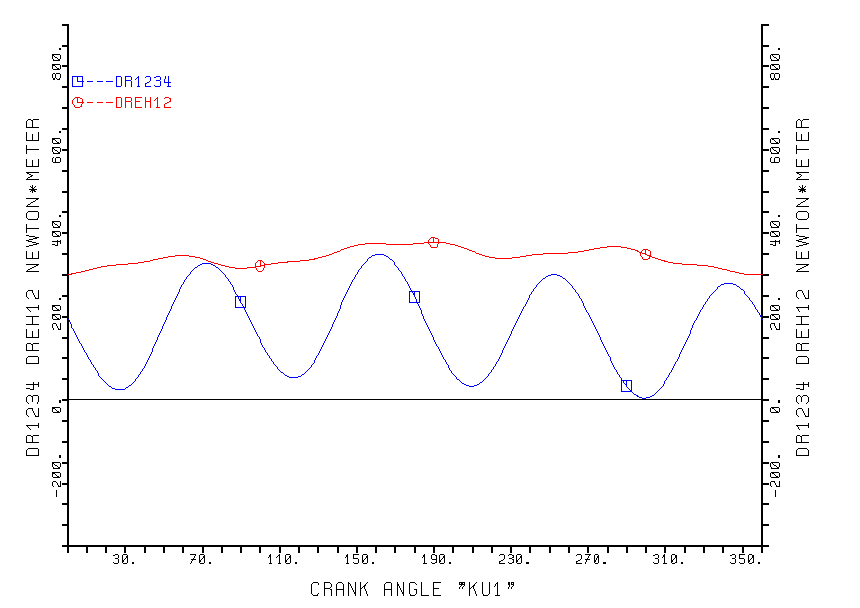
The cyclic torque of this twice double acting engine is always > 0 because of the 4 cycles per crank shaft revolution and is simular to a quadruple sinus-line; (descibed in |11| and to be seen with the program STMOT2) . See   Fig. 5. Here the cyclic torques are calculated for compound fluid.

If 2 of these engines are coupled with a misalignement of Y = 45 (135, 225, or 315) degrees, a nearly constant torque is achieved. -See the upper line in Fig. 5. The fluctuations still to be seen here result from the fact, that the gas loads of the 4 individual partial engines are different because of the not neglectable volume of the piston rods.
The largest gasload is in partial engine "H3-K3" , here the piston rod is of no influence. Engines "H1-K1" and " H2-K2" have the same gasload, here stroke volume in "K1" resp. in "H2" is influenced by the piston rod. Within engine "H4-K4" both cylinders are affected the piston rod, so its gasload is the smalest. As a consequence of this, the torques of the individual engines "H1-K1" , "H2-K2" , "H3-K3" and "H4-K4" are not identical.

press Your browsers Return button to return into previous text

  Back to contents

Fig. 4 shows 3 T-S diagrams. Each for the individual engine with the cylinder pair H1-K1.   Fig. 4a shows the T-S diagram with a gas as the only working fluid. The "frame" in Fig. 4a -as mentioned before- is equal to the ideal Stirling process with the isotherms at the temperatures "TE" and "TC" and with the isochores Vmin and Vmax. The regenerator space "VR" is 0 in this ideal process. Here, the changes of gas state follow one another. The graph within this frame shows the real gas-only process, which has been calculated for the same temperatures "TE" and "TC" as well as for the same working space between Vmin and Vmax, however with a real regenerator space VR > 0 or with some other deadspaces > 0. It touches this frame at the isochore Vmin in accordace with the crank angle position j = 45 degrees at "KU1" and at the isochore Vmax in accordance with the crank angle position j = 225 degrees (at "KU1" ). A curve results here including a smaller area than the frames area,

1.) because of Regenerator and other deadspaces are > 0, and

2.) as the changes of state in the real process do not follow one another as in the ideal process, but overlap here. By the way it is of theoretical interrest to mention, that, if in a real overlaping process the regenerator- and other dead space is = 0, the curve would not only touch the isochores at Vmin and at Vmax but would also touch the isotherm "TE" -at the crank angle position of j = 90 degrees at "KU1" (when the compression space is zero)- and the isotherm "TC" -at the crank angle position of j = 0 degrees at "KU1" (when the expansion space is zero).

  Fig. 4b shows a T2 - S2 diagram of the calculated stirling process for a compound fluid: If water is chosen as working liquid and evaporation positively influenced by large surfaces in the hot expansion cylinders, the total pressure is increased by the vapor partial pressure. This pressure increase results in an increased work per revolution in the engines cylinder pair, which, as illustrated by the graph in   Fig. 4b, is even considerably higher than the efficient work "W i " , of the ideal gas only process, represented by the "frame" in   Fig. 4a. The peaks to be seen in the graph of Fig. 4b are numerical problems: The temperature T2 for compound fluids is defined by the differential equation:

   T2 = ( d Qgas + d Qvapor ) / ( d Sgas + d Svapor)

In the areas, where the addition of the entropie differentials d Sgas + d Svapor
and the addition of the usable thermal energy differentials d Qgas + d Qvapor
come near to zero, these problems arise. The "frame" in   Fig. 4b represents the ideal stirling process for the compound fluid.

  Fig. 4c shows a T3 - S3 diagram of the calculated stirling process for the vapor component only. The frame in Fig. 4c represents the ideal stirling process for the vapor component. The curve within this frame represents the calculation of the real process for the vapor component with VR > 0 and the overlapping changes of state due to the piston movements. Here the temperature T3 is the saturation temperature of the calculated mean partial pressure of the vapor. There are no peaks in this temperature, because T3 is not calculated by a differential equation, but only interpolated from the vapor pressure table.

The thermodynamical equations for the calculation of these T-S and P-V diagrams are published in |11|. Some equations will be found in |3|, |7|, |8|, |9| and |10|.

press Your browsers Return button to return into previous text

  Back to contents

It is necessary to take into consideration that, if a compound working fluid is chosen, the liquid's vapor condenses in the regenerators and compression cylinders. This leads to a transport of the liquid into the compression cylinders. The amount of liquid, transported out of the expansion cylinders, must be returned to these cylinders by a special compensator tube.

The engine presented here is a slowly revolving engine in accordance with the Stirling principle: Well controllable, nearly constant torque, high space ratio, especially suitable for the use of low temperature heat which may be generated by simple solar collectors, few sealing problems. It can be produced easier and cheaper than steam turbines.

press Your browsers Return button to return into previous text

  Back to contents

The engine introduced until now is the twice double acting Stirling engine (see Fig. 1). It consists of 4 individual single acting Stirling engines, resp. it consists of 2 double acting engines. Now we can take one of the double acting engines e.g. "H1-K1 and H2-K2" as the engine; this engine drives the other Stirling machine which now is designed to be a cooling machine, see the following picture:

press Your browsers Return button to return into previous text

  Back to contents

• |1|   J.Bockris,E.Justi: Wasserstoff die Energie fuer alle Zeiten, Konzepte einer Sonnen-Wasserstoff-Wirtschaft, U.Pfriemer Verlag Muenchen, ISBN 3-7906-0092-X 1980.

• |2|   J.Bockris, Energy: The Solar Hydrogen Alternative , Australia & New Zealand Book Co Pty Ltd.

• |3|   R.J.Meijers: Der Philips Stirlingmotor, Motoren Technische Zeits MTZ 29 (1968)/7, DK 621.41/43 (492) Philips

• |4|   H.D. Heck: Der Stirlingmotor, Bild der Wissenschaft 11/1985, ISSN 0006-2375 Deutsche Verlagsanstalt Stuttgart

• |5|   D.Kearney,D.Jaffe: The 80 MWe SEGS units in California, Modern Power Systems, July 1988,Volume 8,Issue 7, ISSN 0260-7840

• |6|   M.Geyer, H.Klaiss: 194 WM Solarstrom mit Rinnenkollektoren, Brennstoff Waerme Kraft Bd.41 1989 Nr.6, VDI Verlag Duesseldorf

• |7|   G. Walker: Stirling Engines, Clarendon Press Oxford 1980

• |8|   P.Fette: Neuer Waermekraftprozess fuer die Nutzung von Niedertemperatur Waerme, Brennstoff Waerme Kraft Bd.39 1987 Nr.11, VDI Verlag Duesseldorf

• |9|   P.Fette: About the Efficiency of the Regenerator in the Stirling Engine and the Function of the Volume Ratio Vmax/Vmin Proceedings of 7'th International Conference on Stirling Cycle Machines ICSC '95  ICSC-95 041 Page 271
    P.Fette: Über den Energieaustausch und die Effektivität des Regenerators in der Stirlingmaschine in bezug auf das Volumenverhältnis V_max / V_min und die Art des Arbeitsfluids.

• |10|   P.Fette: Pressure Computation for a Stirling Engine which work with Compound Fluids. Proceedings of 7'th International Conference on Stirling Cycle Machines ICSC '95  ICSC-95 042 Page 279

• |11|    P. Fette Grundlagen für die Berechnung des Wärmekraftprozesses und der Dynamik von a -Typ Stirlingmotoren mit dem Programm STMOT2

press Your browsers Return button to return into previous text

  Back to contents

  Back to start site

|----------------------------------------------------------------------------------------|
| Crank slot mechanism           | Without steam, only gas   | With steam and gas load   |
|--------------------------------|---------------------------|---------------------------|
|                                | Full load  | Partial load | Full load  | Partial load |
|                                |control vo- | each contr.  |control vo- | each contr.  |
|                 |  Dimension   | lume = 0  %| vol = 25%    |lume = 0%   | vol = 25%    |
|-----------------|--------------|------------|--------------|------------|--------------|
|  Vmax           | Litre        |   2.78     |    3.5       |   2.78     |   3.5        |
|-----------------|--------------|------------|--------------|------------|--------------|
|  Vmax / Vmin:   |   -          |   4.63     |    2.6       |   4.63     |   2.6        |
|-----------------|--------------|------------|--------------|------------|--------------|
|  Pmax           |  Bar         |  16.2      |    7.0       |  17.7      |   8.3        |
|-----------------|--------------|------------|--------------|------------|--------------|
|  Pmax / Pmin    |    -         |   4.7      |    2.6       |   4.0      |   2.3        |
|-----------------|--------------|------------|--------------|------------|--------------|
|  mean torque    | Newton * M   |  41.7      |   15.3       |  89.4      |  45.5        |
|-----------------|--------------|------------|--------------|------------|--------------|
|  Work W         | Newton * M   | 271        |  100         | 569        | 290.0        |
|-----------------|--------------|------------|--------------|------------|--------------|
| e i = W/Wir * 100 |     %        |  54.2      |              | 114.1      |              |
|========================================================================================|
| Connecting rod crank mechanism |                           |                           |
| L/R = 3                        | Without steam, only gas   | With steam and gas load   |
|--------------------------------|---------------------------|---------------------------|
|                                | Full load  | Partial load | Full load  | Partial load |
|                                |control vo- | each contr.  |control vo- | each contr.  |
|                 |  Dimension   | lume = 0  %| vol = 25%    |lume = 0%   | vol = 25%    |
|-----------------|--------------|------------|--------------|------------|--------------|
|  Vmax           | Litre        |   2.9      |    3.7       |   2.9      |   3.7        |
|-----------------|--------------|------------|--------------|------------|--------------|
|  Vmax / Vmin:   |   -          |   4.0      |    2.5       |   4.0      |   2.45       |
|-----------------|--------------|------------|--------------|------------|--------------|
|  Pmax           |  Bar         |  13.5      |    6.5       |  14.9      |   7.8        |
|-----------------|--------------|------------|--------------|------------|--------------|
|  Pmax / Pmin    |    -         |   4.1      |    2.5       |   3.5      |   2.15       |
|-----------------|--------------|------------|--------------|------------|--------------|
|  mean torque    | Newton * M   |  35.8      |   14.2       |  80.6      |  43.4        |
|-----------------|--------------|------------|--------------|------------|--------------|
|  Work W         | Newton * M   | 233.6      |  94.1        | 517        | 278          |
|-----------------|--------------|------------|--------------|------------|--------------|
| e i = W/Wir * 100 |     %        |  47.1      |              | 103.7      |              |
|----------------------------------------------------------------------------------------|

Overall dates for this simulation:

• Cylinder diameters DH = 10 cm, DK = 10 cm
• shift angle between the expansion- and compression cylinders d = -90.0 degrees
• crankradius R = 10 cm
• pistonrod diameter DKST = 2 cm,
• regenerator space VR = 0.15 Litre, regenerator efficiency = 100 %,   no other deadspaces,
• idle pressure P0= 5 bar,
• temperature in expansioncylinders TE = 400 K, in compressioncylinders TC = 300 K.
• This simulation is done at a constant speed, neglecting all friction losses.
  Work and mean torque for the whole 8 cylinder engine must be multiplied by 4 -

The graphs in the following figures are calculated with these overall dates.

press Your browsers Return button to return into previous text

  Back to contents

Fig. 1

Fig. 1

Legend of this drawing:

KW = crankshaft with flywheel,   KU1= lower crankgear, KU2= upper crankgear, M = clutch
H1 : Expansion cylinder, K1 : Compression cylinder of 1'st partial engine
H2 : Expansion cylinder, K2 : Compression cylinder of 2'nd partial engine
H3 : Expansion cylinder, K3 : Compression cylinder of 3'nd partial engine
H4 : Expansion cylinder, K4 : Compression cylinder of 4'nd partial engine
WH1 - WH4 : external heatexchangers for the hot cylinders H1 - H4
WK1 - WK4 : external cooler for the cold cylinders K1 - K4

RC regulator-cylinder (only sketched here for the cold cylinders K4 und K3. For detailed information see the section Power Control

The Regenerator tubes "R" between the hot "H" - and the cold "K"- cylinders are atonce counter flow heat exchangers.

press Your browsers Return button to return into previous text

  Back to contents

press Your browsers Return button to return into previous text

  Back to contents

press Your browsers Return button to return into previous text

  Back to contents

press Your browsers Return button to return into previous text

  Back to contents

press Your browsers Return button to return into previous text

  Back to contents

press Your browsers Return button to return into previous text

  Back to contents

press Your browsers Return button to return into previous text

  Back to contents

press Your browsers Return button to return into previous text

  Back to contents

  Back to start site