Dipl.-Ing. Peter Fette; Am Schäferloch 16; D-75045 Walzbachtal /Germany

 Zurück zum Inhaltsverzeichnis

Kapitel 2.

1. Wärmeübergang und Bestimmung der Temperaturen im Arbeitsfluid

Die Wärmezufuhr auf das Arbeitsgas bzw. seine Kühlung erfolgt durch Beregnung des Gases mit heißer bzw. kalter Arbeitsflüssigkeit und/oder durch Metallspäne, die von dieser Arbeitsflüssigkeit benetzt werden. Siehe bezgl. der Wärmeübertragung auch die allgemeine Beschreibung der Maschine im 1. Teil dieses Berichtes |11|.

Für die Berechnung der Ausdehnungsarbeit und der Wärmeflüsse müssen die Temperaturen des Arbeitsgases in den einzelnen Bereichen der Maschine bekannt sein, die sich aufgrund der Wärmeübergänge zwischen Arbeitsflüssigkeit und Arbeitsgas einerseits sowie infolge der Expansion und der Kompression des Arbeitsgases andererseits einstellen. Ein Modell zur exakten Bestimmung der Temperaturen unter Berücksichtigung dieser Vorgänge ist schwierig zu definieren, und dürfte zudem mit einem erheblichen Rechenaufwand verbunden sein. Die Oberfläche, die Geschwindigkeit und der Abstand der Tröpfchen voneinander sowie die wirksame Oberfläche der Metallspäne sind einige der Größen, die in einem solchen Modell berücksichtigt werden müssen. Die in |7| beschriebene Berechnungsmethode bezieht sich auf den Stirlingmotor USS 4-95 der schwedischen Firma United Stirling. Diese Methode ist hier nicht anzuwenden, da sich der USS 4-95 in seiner klassischen Anordnung von Expansionszylinder - Erhitzer - Regenerator - Kühler - Kompressionszylinder bezgl. der Wärmeübertragung auf das Arbeitsgas nicht mit der hier beschriebenen Maschine vergleichen läßt. Ebenfalls läßt sich das in |8| beschriebene Iterationsverfahren nicht zur Berechnung der Verhältnisse in dieser Maschine anwenden.

In Kapitel 15 wird eine eigene Berechnungsmethode für speziell diese Maschine gezeigt, die den Wärmeübergang infolge Beregnung des Arbeitsfluids analysiert, und die variablen Temperaturen "TE"im Expansionszylinder und "TC" im Kompressionszylinder errechnet.

Die ursprüngliche Absicht war, betreffs der Temperaturen dem Rechenprogramm mehrere Eingabemöglichkeiten anzubieten. Diese Methode soll auch weiterhin ihre Berechtigung haben, obgleich jetzt mit Kapitel 15 eine exaktere Berechnung des Wärmeübergangs und der Temperaturen möglich ist, die auf Computern mit einer CPU Arbeitsfrequenz > 2 Ghz auch in annehmbaren Rechenzeiten Ergebnisse liefert. Denn letztlich ist die in Kapitel 15 beschriebene Methode nur auf den hier vorgestellten Wärmeübergang infolge Beregnung des Arbeitsfluids mit heißer bzw. kalter Arbeitsflüssigkeit anwendbar.

Die bisherige Methode, betreffs der Temperaturen, dem Rechenprogramm mehrere Eingabemöglichkeiten anzubieten, ist vor allem für eine einfache Analyse und graphische Ausgabe der sehr vielen Variablen des Rechenprozesses von Vorteil. Dies soll auch Studierenden helfen, die Vorgänge in der Maschine und die thermodynamischen Besonderheiten des Stirlingprozesses zu verstehen. In diesem Sinne seien 3 Betriebszustände definiert, mit denen das Rechenprogramm arbeiten kann. Mit diesen Betriebszuständen sind die Zustandänderungen bzw. die Temperaturverhältnisse des Arbeitsfluids in den Zylindern gemeint. Denn wenn die Temperaturen bekannt sind bzw. errechnet wurden, können alle anderen Größen des Prozesses ebenfalls berechnet werden.

1. Isotherme Zustandsänderungen im Expansions- und Kompressionszylinder:

   • Die Temperatur des Arbeitsfluids im Expansionszylinder "TE" ist gleich der maximalen Temperatur "TH" der heißen Arbeitsflüssigkeit. Das bedeutet, der Wärmeübergang von der Flüssigkeit auf das Gas ist ideal.

   • Die Temperatur des Arbeitsfluids im Kompressionszylinder "TC" ist gleich der minimalen Temperatur "TK" der kalten Arbeitsflüssigkeit. Das bedeutet, der Wärmeübergang ist im Kompressionszylinder ebenfalls ideal.

   • Die Temperatur des Arbeitsfluids im Expansionszylinder "TE" ist geringer als die optimale Temperatur "TH". Dies ist die Folge des Verlustes beim Wärmeübergang durch die Beregnung des Gases mit heißer Arbeitsflüssigkeit oder die Folge des Verlustes beim Wärmeübergang an den mit heißer Arbeitsflüssigkeit benetzten Metallspänen. Die weitere Rechnung erfolgt mit konstanter Temperatur "TE" < "TH".

   • Die Temperatur des Arbeitsfluids im Kompressionszylinder "TC" ist höher als die optimale Kühlflüssigkeitstemperatur "TK". Dies ist wie im Expansionszylinder die Folge des Verlustes beim Wärmeübergang durch die Beregnung des Gases mit kalter Arbeitsflüssigkeit bzw. des Wärmeübergangs an den mit kalter Arbeitsflüssigkeit benetzten Metallspänen. Die weitere Rechnung erfolgt mit konstanter Temperatur "TC" > "TK". Der Temperaturverlust beim Wärmeübergang an den mit Arbeitsflüssigkeit benetzten Metallspänen kann vom Programm durch eine Energiebilanzrechnung erfaßt werden, die für einen sehr langsam verlaufenden Energieaustausch aufgestellt werden kann. Diese Rechnung erhebt jedoch nicht den Anspruch, die eingangs geschilderte Problematik der exakten Temperaturbestimmung zu lösen.

2. Die Temperaturen im Expansions- und Kompressionszylinder können jeweils als Differenz DT zu den optimalen Temperaturen "TH" und zu "TK" quasi als Temperaturprofile DTE = TH-TE und DTC = TC-TK eingegeben werden. Damit besteht die Möglichkeit, die Berechnung an gemessenen Werten zu überprüfen.

3. Das Programm rechnet mit polytropen Zustandsänderungen im Expansions- und Kompressionszylinder. Dabei kann "TE" < "TH" und auch > "TH" werden, und "TC" kann > "TK" und ggf. auch < "TK" werden. Hier wird zur Vereinfachung der Rechnung die gesamte Wärmeübertragung und auch der Energieverlust durch Wärmeleitung in den Zylinderwänden durch einen entsprechend angepaßten Polytropen Exponenten "m" erfaßt. Der Wärmeübergang auf das Arbeitsfluid erfolgt wie oben beschrieben durch Beregnung des Gases und/oder durch benetzte Metallspäne.

Alle Rechenergebnisse, die auf isothermen Zustandsänderungen -also auf dem idealen Betriebszustand- beruhen, z.B. die zeitlichen oder Kurbelwinkel bezogenen Verläufe von Drehmoment, Wärmeflüsse, Ausdehnungsarbeit u.a., sind gedacht als Beitrag zum besseren Verständnis dieser Maschine. Sie weisen aber auch -z.B. beim Ausnutzungsgrad, oder dem erzielbaren Volumenverhältnis in Verbindung mit dem Verlauf der Heizleistung- allgemein gültig auf die Grenzen einer α-Typ Stirlingmaschine hin.

Die Ermittlung der Wärmeflüsse, des Druckverlaufs, der Ausdehnungsarbeiten, der Drehmomente, der Dynamik u.a., ist der Versuch, (wenn polytrope Zustandsänderungen geschehen, mit relativ geringem Rechenaufwand und bei Anwendung der Rechenmethode nach Kapitel 15 mit deutlich höherem Rechenaufwand) den wirklichen Verhältnissen in dieser Maschine näher zu kommen.

Erläuterungen zu der polytropen Zustandsänderung in dieser Maschine:

Selbst wenn der Wärmeübergang durch Beregnung des Arbeitsgases erfolgt und auch noch durch zusätzliche Wärmeübertragungsflächen weiter verbessert wird, werden sich keine konstanten (isothermen) Temperaturen im Expansions- bzw. im Kompressionszylinder einstellen. Diese sind letztlich polytrope Zustandsänderungen, die sich aber deutlich von adiabaten Zustandsänderungen unterscheiden: Die adiabate Zustandsänderung gehorcht der Gleichung

(1.1)

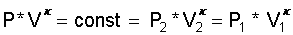
Kennzeichen der adiabaten Zustandsänderung ist, daß während der Volumenänderung einer konstant bleibenden Gasmasse keine Wärmezufuhr bzw. kein Wärmeentzug stattfindet. Dann ist der Adiabatenexponent k für ideale Gase definiert als das Verhältnis der spezifischen Wärme bei konstantem Druck c_p zur spez. Wärme bei konstantem Volumen c_v.

(1.2)

Die adiabate Zustandsänderung ist der eine kaum zu erreichende und auch nicht erwünschte Extremfall, und die isotherme Zustandsänderung, die der Gleichung

(1.3)

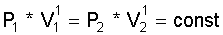
gehorcht, ist der andere kaum erreichbare aber wünschenswerte Extremfall.

Die sich in dieser Maschine einstellende Zustandsänderung wird durch die stetige Wärmezufuhr im Expansionszylinder und durch den stetigen Wärmeentzug im Kompressionszylinder sowie durch die Expansion und die Kompression des Arbeitsgases bestimmt. Die Wärmeübertragung ist infolge des flüssigen Übertragungsmediums "temperaturgeprägt". So werden sich - anders als bei Brenner beheizten Gaserhitzern (siehe auch |7|) - hier nicht so starke Temperaturänderungen im Arbeitsfluid weder bei der Kompression noch bei der Expansion ergeben. Es erscheint gerechtfertigt, die Temperaturverhältnisse in den Zylindern mit der Gleichung für polytrope Zustandsänderungen zu beschreiben:

(1.4)

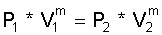
Der Polytropenexponent "m" kann sich in den Grenzen bewegen:

(1.5)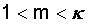

Mit "m" = 1 würde sich die Isotherme Gl.(1.3) ergeben und mit "m" = k ergibt sich die Adiabatengleichung Gl.(1.1).

Für die hier vorliegende temperaturgeprägte Wärmeübertragung im Expansions- und im Kompressionszylinder, wobei immer optimale Wärmeübertragungsflächen zur Verfügung stehen, kann man von einem Polytropenexponenten "m", der nahe bei "1" liegt ausgehen. "m" sollte experimentell bestimmt werden. Es ist anzunehmen, daß "m" nicht konstant sondern auch eine Funktion des Kurbelwinkels ist. Bei genügend guter Isolation der Expansionszylinderwände können auch die immer noch vorhandenen geringen Wärmeleitungsverluste in dem experimentell ermittelten Polytropenexponenten mit erfaßt werden.

Aus Gl.(1.4) lassen sich für die Temperaturen folgende Beziehungen ableiten:

(1.6)

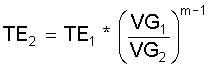
(1.7)

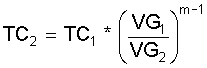
mit "VG" dem Gesamtvolumen nach Gl.(2.8). Die Indizes 1 und 2 zeigen auf den Anfangs- und Endzustand des Rechenschrittes für die jeweiligen Größen.

Ein Schönheitsfehler diese Modells ist, daß die Anfangstemperaturen TE₁und TC₁ geschätzt werden müssen. Das Programm ist erst mit der in Kapitel 15 beschriebenen Methode in der Lage, ein dynamisches Hochfahren der Maschine zu simulieren, ausgehend von einer Ausgangstemperatur "TH" im Expansionszylinder und "TK" im Kompressionszylinder zum Zeitpunkt "0".

Waehlen Sie den Zurueck Schalter Ihres Browsers, um an die vorherige Textstellen zurueck zu kommen.

Kapitel 2.

 Zurück zum Inhaltsverzeichnis