Dipl.-Ing. Peter Fette; Am Schäferloch 16; D-75045 Walzbachtal /Germany
Bei hinreichend geringer Drehzahl lassen sich mit genügender Genauigkeit quasi-statische Druckverhältnisse, Wärmeflüsse, Leistung und Drehmomente dieser Stirlingmaschine nach Abb.1 über das ideale Gasgesetz errechnen. Ausgehend von einer Teilmaschine mit nur 1 zusammenwirkenden Zylinderpaar H1-K1 und zugehörigem Regenerator, werden jeweils um die Kurbelwellenumdrehung von j = 90, 180 und 270 Grad verschoben, in den anderen 3 Teilmaschinen die gleichen Bewegungs- und Druckverhältnisse ablaufen. Durch Überlagerung der Kräfte, die auf die Kolben wirken, ergeben sich die resultierenden Kräfte für beide Kolbenstangen und somit ein resultierendes Drehmoment für die ganze 8 Zylinder Maschine. Folgende 7 Annahmen werden für die Berechnung des Arbeitstaktes gemacht; diese Annahmen gelten allgemein und hier im besonderen für den "nur Gas" Betrieb der Maschine. Für ein Arbeitsfluid, das aus Gas + Dampf besteht ("compound fluid") müssen betreffs der Dampfkomponente noch weitere 4 Annahmen gemacht werden, die in Kapitel 11 beschrieben sind.
Es gilt das ideale Gasgesetz.
Die Bewegung sei so langsam, daß Druckverluste in der Flüssigkeits- und in der Gasströmung vernachlässigt werden können. Wie die Massenkräfte der hin und her schwingenden Arbeitsflüssigkeit, sowie die bei höheren Drehzahlen nicht zu vernachlässigenden Reibungsverluste berücksichtigt werden, wird in Kapitel 13) behandelt.
Betrachtet wird das Zylinderpaar H1-K1 mit zugehörigem Regenerator. Der Wärmeübergang im Expansionszylinder "H1" erfolgt wie in Kapitel 1 beschrieben. Das Gas hat hier die Temperatur "TE". Der Zylinderdurchmesser ist im Gas- und Flüssigkeitsbereich konstant und ist gleich dem Kolbendurchmesser "DH". Daraus resultiert die Zylinder- bzw. Kolbenquerschnittsfläche:
(2.1.1)
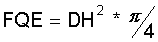
Bei den Teilmaschinen, wo die Querschnittsfläche der Kolbenstange mit ihrem Durchmesser "DKST" das Expansionsvolumen beeinträchtigt, ist die wirksame Zylinderquerschnittsfläche:
(2.1.2)
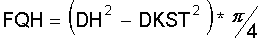
Der Kompressionszylinder "K1" wird wie in Kapitel 1 beschrieben gekühlt. Das Gas hat hier die Temperatur "TC". Auch hier ist der Zylinderdurchmesser im Gas- und Flüssigkeitsbereich konstant und ist gleich dem Kolbendurchmesser "DK". Die wirksame Kolbenquerschnittsfläche "FQK" ist jedoch reduziert um die Querschnittsfläche der Kolbenstange mit ihrem Durchmesser "DKST".
(2.2.1)
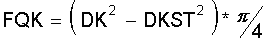
Bei den Teilmaschinen, wo die Kolbenstange das Kompressionsvolumen nicht beeinträchtigt, ist die wirksame Zylinderquerschnittsfläche:
(2.2.2)
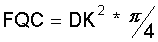 .
.
Der Regenerator ist -siehe Abb.1- im Gegensatz zu sonst üblichen Regeneratoren hier ein relativ langes Verbindungsrohr zwischen dem Expansionszylinder H1 und dem Kompressionszylinder K1 ohne irgendwelche Metallgewebeeinlagen, jedoch mit rauher Oberfläche. Der Energieaustausch, der sonst üblicherweise über die Beladung und Entladung der Metallgewebemasse erfolgt, muß bei dem hier verwendeten Regeneratorrohr über die rauhe Oberfläche des langen Rohres erfolgen. Eine zusätzliche Hilfe ist hier die Gegenstrom - Wärmeaustauschmöglichkeit zweier koaxial ineinanderliegender Regeneratorrohre der jeweils doppelt wirkenden Teilmaschinen mit den Zylinderpaaren H1-K1 und H2-K2 sowie H3-K3 und H4-K4. Das Temperaturprofil des Arbeitsgases längs des Regeneratorrohres dürfte sich in Abhängigkeit von Richtung und Geschwindigkeit des Gasmassenstromes sowie von der Oberflächenbeschaffenheit des Rohres kontinuierlich ändern.
Hier sei die Annahme gemacht, daß das Temperaturprofil linear verläuft zwischen den Endtemperaturen des Regenerators; wobei als "Endtemperatur" die Temperatur gemeint ist, die sich im Gasmassenteilchen einstellt, wenn es den Regenerator am heissen Ende bei Eintritt in den Expansionszylinder verläßt -im Idealfall mit TE- , bzw. wenn es den Regenerator am kalten Ende bei Eintritt in den Kompressionszylinder verläßt -im Idealfall hier mit TC. Wie bei einem verlustbehafteten Regenerator zu rechnen ist, wird in Kapitel 8 und in 11 beschrieben.
Das Gasvolumen "VR" im Regenerator ist konstant. Die Temperatur des Gases im Volumen "VR" wird hier als eine mittlere Temperatur "TR" angesetzt. Diese ist im verlustlosen Regenerator definiert als der logarithmische Mittelwert (s.|8|) zwischen TE und TC zu:
(2.3)
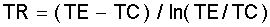
Im Ruhezustand (bei entkoppelten Kurbeltrieben Ku1 und Ku2, beide mit gleichem Kurbelwinkel von φ = - 90 Grad) sei die Gastemperatur überall "T0". Das Gasvolumen im Expansionszylinder H1 ist dann: VE0 = FQE x R, dazu kommt das Totvolumen im Expansionszylinder VH00E. Das Gasvolumen im Kompressionsylinder K1 ist dann: VC0 = FQK x R, dazu kommt das Totvolumen im Kompressionszylinder VH00C. Der Kurbelradius "R" ist für beide Kurbeltriebe gleich groß. Ausgangsdruck in diesem Ruhezustand ist "P0". Dann errechnet sich die Gasmasse MG nach dem idealen Gasgesetz; mit "RG" = Gaskonstante, und dem Ausgangsvolumen "V0"
(2.4)
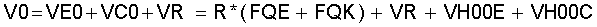
(2.5)
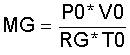
Im Betriebszustand drehen die Kurbeltriebe im Uhrzeigersinn, dabei erfährt der Kurbeltrieb Ku2 um den Versatzwinkel δ = 90 Grad später den gleichen Bewegungsablauf wie der Kurbeltrieb Ku1. Die Kolbenbewegung erfolge rein sinusförmig mittels eines Kurbelschleifentriebs. Mit dem Kurbelwinkel φ ergibt sich für das Expansionsvolumen VE in Zylinder H1 inklusive eines einstellbaren Totvolumens im Expansionszylinder VH00E
(2.6a)

Das Kompressionsvolumen VC in K1 unter Berücksichtigung des Versatzwinkels δ errechnet sich inklusive des einstellbaren Totvolumens im Kompressionszylinder VH00C zu:
(2.7a)
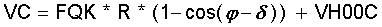
Die Verminderung des Kompressionsvolumens um das Volumen der Kolbenstange wird -siehe oben- in FQK berücksichtigt.
Wie der Kurbelschleifentrieb nach Abb.1 aussehen kann, vermittelt folgende Abbildung; das 1. Lagerschild ist hier zugunsten der Sichtbarkeit der Kurbelschwinge ausgeblendet worden:
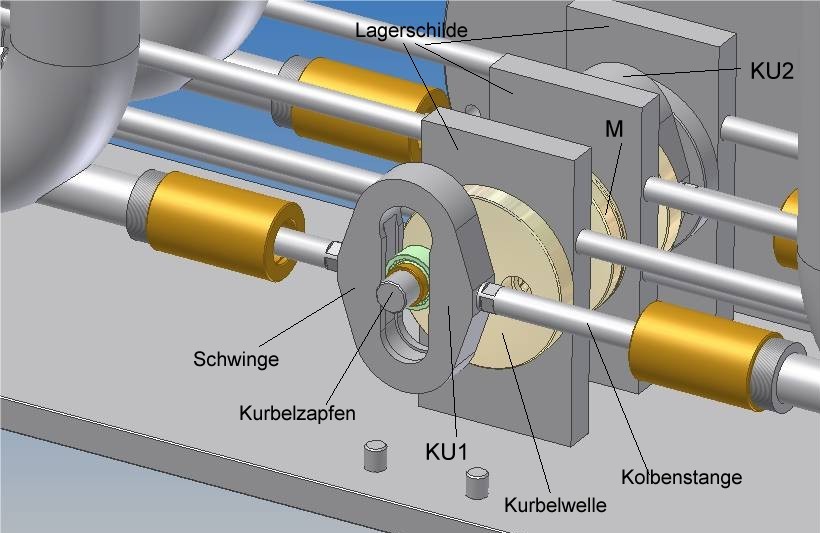
Im Prototyp ist die Kurbelschwinge folgendermaßen realisiert worden:

Anstelle von VE und VC nach Gleichungen Gl.(2.6a) und Gl.(2.7a) ergäbe sich für einen Pleuelstangen Kurbeltrieb:
(2.6b)
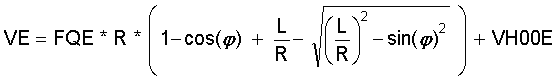
(2.7b)
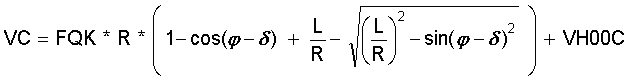
mit L = Länge der Pleuelstange, R = Radius des Kurbeltriebes.
Soll Teillast gerechnet werden -siehe "Regelung der Maschine" in |9|-, dann wird zu VE das Regelvolumen RVE und zu VC das Regelvolumen RVC hinzu addiert. Diese Regelvolumina vergrössern das Totvolumen. Sie werden aber zu den Zylindervolumina gerechnet, da in RVE die selbe Temperatur wie in VE, und in RVC die selbe Temperatur herrschen soll wie in VC. Mit diesen Regelvolumina ergeben sich für die Maschine mit Kurbelschleifentrieb:
(2.6)
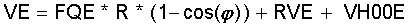
und
(2.7)
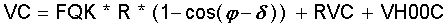
Die Maschine ist mit einer Drehzahl n < 300 U/min ein Langsamläufer. Unter Vernachlässigung der Strömungswiderstände im Regenerator herrscht in der Teilmaschine H1-K1, bzw. in den Volumina VE,VC und in VR dieser Teilmaschine immer der gleiche Druck P. In diesem Gesamtvolumen
(2.8) VG = VE + VR + VC
ist die gesamte Gasmasse MG aufgeteilt in:
(2.9) MG = ME + MC + MR
ME = Gasmasse im Expansionsvolumen VE im Zylinder H1; MC = Gasmasse im Kompressionsvolumen VC im Zylinder K1; MR = Gasmasse im Regenerator im Volumen VR. Es ergibt sich der gemeinsame Gasdruck P in den 3 Volumina der Teilmaschine jeweils mit dem idealen Gasgesetz errechnet zu:
(2.10)
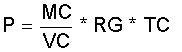
(2.11)
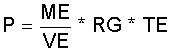
(2.12)
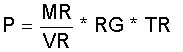
Durch Substitution und Umformung der Gleichungen Gl.(2.5) und Gl.(2.9) bis Gl.(2.12) erhält man:
(2.13)
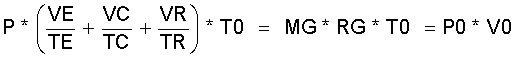
Der Ausdruck (VE/TE + VC/TC + VR/TR) * T0 wird auch das auf die Temperatur T0 normierte Gesamtvolumen V genannt |1|.
(2.14)
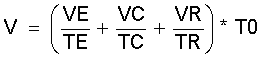
Somit ergibt sich der Druck bei dem vorausgesetzten vollkommenen Druckausgleich in den Gasräumen VE, VC und VR dieser Teilmaschine, also in einem zusammenwirkenden Zylinderpaar mit dem zugehörigen Regenerator zu:
(2.15)
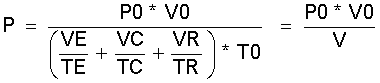
oder mit den Beziehungen für die Gasmasse ist
(2.16)
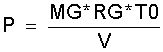
Der Druck P nach den Gleichungen Gl.(2.15) oder Gl.(2.16) ist bei konstanten Temperaturen TE und TC mit den Gleichnungen Gl.(2.6a) für VE und Gl.(2.7a) für VC nur vom Kurbelwinkel φ abhängig. Abb.2. Bei polytroper Zustandsänderung ergeben die Temperaturänderungen stärkere Druckschwankungen in der Maschine. Mit P und dem Gesamtvolumen VG läßt sich das P-V Diagramm -Abb.3- zeichnen und die Arbeit errechnen, die pro Kurbelwellenumdrehung von der Teilmaschine H1-K1 abgegeben wird. Hier wird zwischen der Arbeit im Expansionszylinder und der Arbeit im Kompressionszylinder unterschieden. In Differentialform:
(2.17) d_AE = P * d_VE ist das Differential der Ausdehnungsarbeit im Expansionszylinder
(2.18) d_AC = P * d_VC ist das Differential der Ausdehnungsarbeit im Kompressionszylinder
d_A ist das Differential der Nutzarbeit als Summe beider Ausdehnungsarbeiten:
(2.19) d_A = d_AE + d_AC = P * d_VE + P * d_VC = P * d_VG
In Abb.3a werden d_AE, d_AC sowie deren Integrale AE und AC für isotherme Verhältnisse dargestellt.
Die gesamte Ausdehnungsarbeit während eines Arbeitstaktes, d.h. während einer Umdrehung der Maschine ist das Integral von Gl.(2.19) über die Umdrehungszeit:
(2.20)
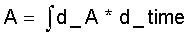
Waehlen Sie den Zurueck Schalter Ihres Browsers, um an die vorherige Textstellen zurueck zu kommen