Dipl.-Ing. Peter Fette; Am Schäferloch 16; D-75045 Walzbachtal /Germany

 Zurück zum Inhaltsverzeichnis

Kapitel 10
weiter zu Kapitel 12

  11. Berechnung der Wärmeflüsse und der Druckerhöhung, wenn das Arbeitsfluid aus "Gas + Sattdampf " zusammengesetzt ist.

• 11.1. T3-S3 Diagramm für den Stirling Prozeß mit Sattdampf als Arbeitsfluid
   
• 11.2. T2-S2 Diagramm für den Stirling Prozeß mit einem Arbeitsfluid aus "Gas + Sattdampf "
   

Falls in der hier beschriebenen Maschine eine Arbeitsflüssigkeit mit einem für die Temperatur im Expansionszylinder genügend hohen Dampfdruck gewählt wird, muß der Dampfpartialdruck "Ps" dieser Flüssigkeit berücksichtigt werden. Es wirkt dann ein aus Gas und Sattdampf zusammengesetztes Arbeitsfluid. Bei Walker |3| wurde darauf schon eingegangen und die Nützlichkeit eines "compound working fluid" beschrieben. Eine reale Maschine, die mit "compound working fluid" arbeitet, sowie die Berechnung eines solchen Prozesses konnten noch nicht gezeigt werden. Man wollte auch eine Maschine mit überhitztem Dampf betreiben. Die hier beschriebene Maschine weicht in diesem konkreten Punkt von dieser Vorstellung ab, sie kann nur mit gesättigtem Dampf arbeiten. Ihr Arbeitsprozeß läßt sich vollständig berechnen.

Insgesamt sind 3 Druckzustände für Gas und Dampf zu unterscheiden:

1. Der minimale Gasdruck "Pgas _min " in der Maschine ist immer höher als der maximale Sattdampfdruck "PSTE" bei der Temperatur "TE" im Expansionszylinder. : PSTE < Pgas _min
2. Der Dampfpartialdruck im Expansionszylinder "PSTE" ist größer als der maximale Gasdruck " Pgas _max". PSTE > Pgas_max. In diesem Fall würde im Expansionszylinder und ggf. auch in den heißen Bereichen des Regenerators im wesentlichen nur Dampf sein, der sich auch im überhitzten Zustand befinden kann. Ein Stirlingmotor, der sich in diesem Betriebszustand befindet, unterscheidet sich kaum von einer schlechten Dampfmaschine mit Lufteinschluß im Kondensator.
3. Der Dampfdruck "PSTE" im Expansionszylinder liegt im Bereich des Gasdruckes: Pgas _min < PSTE < Pgas _max . In diesem Fall kann sich im Expansionszylinder und ggf. auch in den heißen Bereichen des Regenerators keine Gasströmung wie im 1. Fall ausbilden. Das gesamte Druckverhältnis P _max / P _min wird kleiner als im 1. Fall und damit wird auch die Arbeitsausbeute je Umdrehung kleiner, was nicht wünschenswert ist.

PSTE < Pgas _min

Der in die Berechnung der Ausdehnungsarbeit nunmehr eingehende Gesamtdruck P -Abb.12a- ergibt sich dann aus den Partialdrücken der Gas- und Sattdampfkomponenten.

(11.1) P = Pgas + Ps

Wie die Arbeitsausbeute in der Maschine durch die Drucksteigerung um den Dampfpartialdruck "PS" erhöht wird, zeigen die P-V Diagramme in Abb.12.

Durch Experiment und Simulationsrechnung hat sich ergeben, daß der Dampfpartialdruck "Ps" folgendermaßen berechnet werden kann: (Dabei wird wie bei nur Gas als Arbeitsfluid vollkommener Druckausgleich in der Maschine angenommen). Ausgehend von folgenden Definitionen:

PSTC = Sättigungsdruck des Dampfes bei der Temperatur TC im Kompressionszylinder
PSTE = Sättigungsdruck des Dampfes bei der Temperatur TE im Expansionszylinder
PSTR = Sättigungsdruck des Dampfes bei der mittleren Temperatur TR im Regenerator.

"P" ist bei vollkommenen Druckausgleich der Gesamtdruck in den 3 Volumina der Maschine:

• im Expansionszylinder:

      (11.2) P = Pgas _E + PSTE = ME/VE * RG * TE + PSTE

                 Daraus ergibt sich für die Gasmasse im Expansionszylinder:

      (11.3) ME = (P - PSTE) * VE / (RG * TE)

• im Kompressionszylinder:

      (11.4) P = Pgas _C + PSTC = MC/VC * RG * TC + PSTC

                 Daraus ergibt sich für die Gasmasse im Kompressionszylinder:

      (11.5) MC = (P - PSTC) * VC / (RG * TC)

• im Regenerator:

      (11.6) P = Pgas _R + PSTR = MR/VR * RG * TR + PSTR

                 Daraus ergibt sich für die Gasmasse im Regenerator:

      (11.7) MR = (P - PSTR) * VR / (RG * TR)

Mit der Beziehung für die gesamte Gasmasse Gl.(2.9) MG  = ME + MC + MR   = P0 * V0 / (RG * T0) kann der Gesamtdruck "P" aus den Gl.(11.3), Gl.(11.5) und Gl.(11.7) errechnet werden über:

(11.8)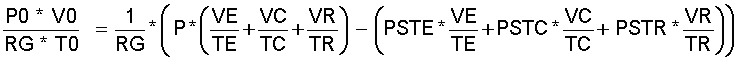    

zu:

(11.9)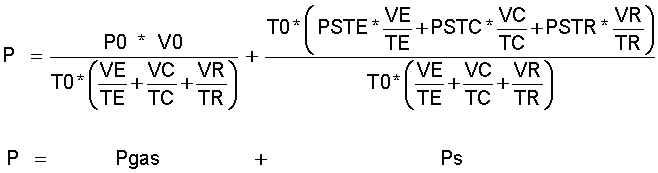     

Mit "V" dem auf die Temperatur T0 bezogenem Gesamtvolumen -siehe Gl.(2.14)- ist der Dampfpartialdruck "PS" unter der Voraussetzung des vollkommenen Druckausgleichs in der Maschine:

(11.10)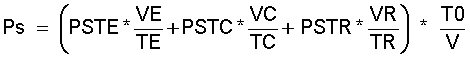  

Da die Temperatur im Regenerator von TC über TR bis TE reicht (im verlustbehafteten Regenerator von TCR über TR bis TER), und die Dampfdruckkurve nicht linear verläuft, ist es zweckmäßig, den Regenerator in mehrere (mindestens 3) Temperaturzonen zu unterteilen. Auch hier soll die in Kapitel 2 beschriebene Annahme des linearen Temperaturverlaufs im Regenerator gelten. Dann können 3 gleiche Temperaturzonen in jeweils 3 gleichen Regeneratorvolumina VR/3 definiert werden. In jeder dieser Temperaturzonen existiert eine Temperaturdifferenz von TEMTC3 = (TE-TC)/3 bzw. TEMTC3 = (TER - TCR)/3 im verlustbehafteten Regenerator. Die Ableitung der Regeneratortemperatur |8| -siehe Gl.(2.3)- als log. Mittelwert geht vom idealen Gasgesetz aus. Wendet man das ideale Gasgesetz auf Sattdampf an, so ist in dem bei dieser Maschine infrage kommenden Temperaturbereich von 20 bis 150 Grad C schon mit einem Fehler von ca. 5% zu rechnen.

TRM1 = das log. Mittel der Temperatur im heißen Teil des Regenerators ist dann:

(11.11)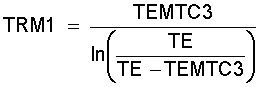   

TRM2 = das log. Mittel der Temperatur in der Mitte des Regenerators:

(11.12)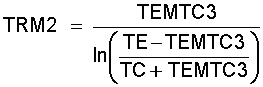   

TRM3 = das log. Mittel der Temperatur im kalten Teil des Regenerators:

(11.13)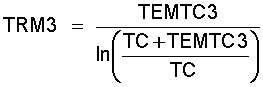   

Für den verlustbehafteten Regenerator müssen statt TE --> TER und statt TC --> TCR gesetzt werden.

Für diese 3 Regenerator Temperaturen werden die Sättigungsdrücke PSR1, PSR2, PSR3 berechnet. Dann ergibt sich der mittlere Sättigungsdruck Ps genauer zu:

(11.14)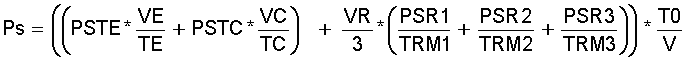   

Mit diesem mittleren Dampfpartialdruck Ps und dem Gesamtvolumen VG eines zusammenwirkenden Zylinderpaares mit zugehörigem Regenerator kann ein P-V Diagramm für die Dampfkomponente im Stirling Prozeß erstellt werden; siehe Abb.12.

-

  11.1 T3-S3 Diagramm für den Stirling Prozeß mit Sattdampf als Arbeitsfluid

Für ein T-S Diagramm nur für die Dampfkomponente, dem T3 - S3 Diagramm, läßt sich für den mittleren Dampfpartialdruck Ps nach Gl.(11.14) aus der Dampfdruckkurve eine Sättigungstemperatur des Dampfes "T3" ablesen, bzw. berechnen.

Zur Berechnung der Entropie "S3" folgende Überlegungen:

Aus der Sattdampfdichte r_T3 bei T3 und dem Gesamtvolumen VG ist eine mittlere Sattdampfmasse SDM definiert. SDM = f(Ps,T3,VG).

(11.15)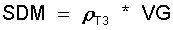   

Mit den Werten für gesättigten Dampf bei der Temperatur T3 läßt sich jetzt für jeden Rechenschritt ähnlich wie für den "nur Gas" Betrieb der Maschine (siehe auch Kapitel 7) eine Energiebilanz erstellen. Anstelle der inneren Energie "U" rechnet man hier zweckmäßigerweise mit der Enthalpie "I" des Dampfes.

Die einem geschlossenen Kreisprozeß übertragene (oder entzogene) thermische Energie hat eine Änderung der Enthalpie des Arbeitsfluids zur Folge und kann bewirken, daß das Arbeitsfluid Arbeit verrichtet. Bezogen auf die Dampf-Komponente des Arbeitsfluids läßt sich dies in Differentialform ausdrücken:

(11.16)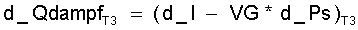   

mit d_I = dem Differential der Dampfenthalpie bei der jeweiligen Temperatur T3 und Ps dem Sättigungsdruck bei T3; VG * d_Ps ist die "Arbeit" des Sattdampfes. Die Dampfenthalpie I_T3 ergibt sich mit der Sattdampfmasse SDM zu

(11.17)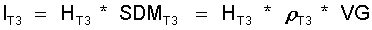   

Mit H_T3 der Verdampfungswärme, und r_T3 der Sattdampfdichte jeweils bei der Temperatur T3.

Die Entropieänderung ergibt sich zu:

(11.18)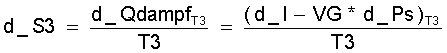   

Für eine genügend kleine Rechenschrittweite ergibt sich d_I_T3 zu:

(11.19)

Die Berechnungsmethode geht von 4 idealisierten Voraussetzungen aus:,

1. Es bildet sich ein mittlerer Dampfdruck in allen Räumen der Maschine aus, der von den Temperaturen und den Volumina abhängig berechnet wird zu:

   (11.10)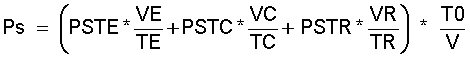   

   Siehe Gl.(11.10) oder Gl.(11.14). Diesem Dampfdruck entspricht eine mittlere Sattdampftemperatur "T3", "T3" kann den Dampf-Tafeln entnommen, oder berechnet werden. |4|

2. Es bildet sich immer nur soviel Sattdampfmasse, wie es der Temperatur T3 und dem momentanen Gesamtvolumen VG entspricht; im Gegensatz zu der bei Walker |3| gemachten Annahme ist hier das Verhältnis Dampfmasse zu Gasmasse nicht konstant.

3. Das Kondensat wird nicht transportiert. Der Dampf entsteht und kondensiert an den jeweiligen Temperaturgrenzen zwischen den 3 Räumen: Expansionszylinder, Regenerator und Kompressionszylinder. (Die Energieverluste, die durch den real stattfindenden Transport von Dampf und Kondensat entstehen, werden gesondert errechnet, siehe Kapitel 12 und Gl.(12.1); sie sollen hier zunächst nicht berücksichtigt werden.)

4. Für die Dampfkomponente ist der Regenerator unwirksam.

Die Integration bzw. die Aufsummierung von d_S3 zu S3 und die mittlere Sättigungstemperatur T3 ergeben das T3-S3 Diagramm für die Dampfkomponente des Arbeitsfluids in der realen Maschine mit Kurbeltrieb. Abb.7

Berechnung des T3-S3 Diagramms für die Dampfkomponente im idealen Stirling Prozess

Die Entropierechnung für die Dampfkomponente des idealen Stirlingprozeß ergibt im T3-S3 Diagramm Abb.7 ähnlich wie beim reinen Gasbetrieb (T-S1 Diagramm) eine Art "Rahmen", der die Kurve umhüllt, die sich aus der oben gezeigten Entropieberechnung für die reale Maschine mit Kurbeltrieb ergibt. Die Berechnung der Kurven erfolgt immer aus der Energiebilanz Gleichung Gl.(11.16), (Verdampfung und Druckerhöhung sowie Kondensation und Drucksenkung) wobei im idealen Stirlingprozeß , wo Expansion und Kompression in einem Zylinder erfolgen können, die oben gemachten Annahmen ja auch gültig sind, da hier kein Hin- und Herschieben des Arbeitsfluids erfolgen muß.

Da die Dampfmasse SDM im idealen Stirlingprozeß nicht konstant bleibt, ist sie wie auch in der vorherigen Rechnung in die Differentiation miteinzubeziehen. Man unterscheidet auch hier -ähnlich wie beim idealen Stirlingprozeß mit nur Gas als Arbeitsfluid (Gl.(9.4))- die beiden Anteile:

d_S3t bei der isochoren Zustandsänderung -die Temperatur ändert sich, und
d_S3v bei der isothermen Zustandsänderung. -das Volumen ändert sich.

(11.20)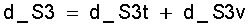   

1) d_S3t die Entropieänderung während der isochoren Wärmezufuhr (bzw. -entzug) :

a) bei VG _min nach Gleichung Gl.(11.18):

(11.18-)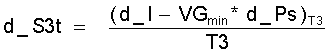

mit d_I nach Gl.(11.19) oder, wenn die Entropien von Dampf und Flüssigkeit vorliegen:

(11.21)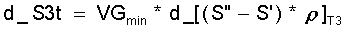

S"= Entropie des Dampfes bei T3
S'= Entropie der Flüssigkeit bei T3
r = Sattdampfdichte bei T3
T3 von TC bis TE

b) bei VG _max nach Gleichung Gl.(11.18):

(11.18-)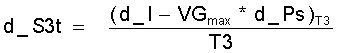

mit d_I nach Gl.(11.19) oder, wenn die Entropien von Dampf und Flüssigkeit vorliegen:

(11.22)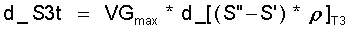

2) d_S3v die Entropieänderung während der isothermen Zustandsänderung

Ausgehend von Gl.(11.18):

Da hier der Dampfdruck konstant ist, entfällt der Ausdruck VG * d_Ps und d_S3v nach Gl.(11.18) vereinfacht sich.

a) Bei der isothermen Expansion für T3 = TE. Da H und r konstant sind, kann d_I unmittelbar durch Differentiation von Gl.(11.17) gewonnen werden. d_I braucht hier nicht nach Gl.(11.19) errechnet zu werden.

(11.23)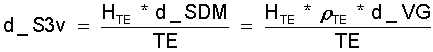

d_S3v nach Gl.(11.23) kann sogleich integriert werden:

(11.24)

oder, wenn die Entropien von Dampf und Flüssigkeit vorliegen (S" und S' sind konstant):

(11.25)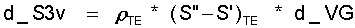

Die Integration von Gl.(11.25) ergibt:

(11.26)

b) Bei der isothermen Kompression für T3 = TC, (H und r sind konstant) ergibt sich:

(11.27)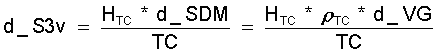

Die Integration von Gl.(11.27) ergibt:

(11.28)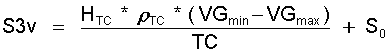

oder, wenn die Entropien von Dampf und Flüssigkeit vorliegen:

(11.29)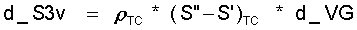

Die Integration von Gl.(11.29) ergibt:

(11.30)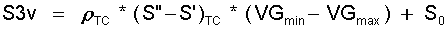

Mit VG in den Grenzen von: V_min ≤ VG ≤ V_max ;
  Sattdampfdichte r_TE und r_TC sowie
  Verdampfungswärme H_TE , H_TC , und die
  Entropien S" und S' bei den jeweiligen Temperaturen TE bzw bei TC.

Für die Konstruktion der T3 - S3 Diagramme gilt das gleiche wie im Kapitel 9 gesagt für die T - S1 Diagramme.

-

  11.2 T2-S2 Diagramm für den Stirling Prozeß mit einem Arbeitsfluid aus "Gas + Sattdampf "

Für den idealen Stirling Prozeß mit einem Arbeitsfluid aus Gas und Sattdampf ergibt sich ein T2 - S2 Diagramm, in dem die Entropie S2 zusammengesetzt ist aus den Entropieen beider Einzelkomponenten. Diese "Kurve" bildet wiederum einen Rahmen um das T2-S2 Diagramm des realen Prozesses. In Differentialform ergibt sich d_S2 zu:

(11.31) d_S2 = d_S1 + d_S3 = d_S1v + d_S1t + dS3v + d_S3t

Mit T2 in den Grenzen von: TC ≤ T2 ≤ TE .

Für den realen Prozeß einer Maschine mit Kurbeltrieb und Regeneratorvolumen VR > 0 lassen sich die P-V Diagramme und T-S Diagramme sowohl für den Prozeß mit dem aus Gas + Sattdampf zusammengesetzten Arbeitsfluid, als auch für die zwei Teilprozesse -einen mit Gas und den anderen mit Sattdampf als Arbeitsfluid- erstellen. Die eingeschlossenen Flächen der Diagramme entsprechen einander. Das heißt: Die Arbeit pro Kurbelwellenumdrehung integriert aus der T-S1 Diagramm Kurve für den reinen Gasbetrieb addiert mit der Arbeit aus der Integration der T3-S3 Diagrammkurve für den reinen Sattdampfbetrieb ist bis auf die Stoffwerte- und Rechengenauigkeit gleich der Arbeit, die sich aus der Integration des P-V Diagramms für den gemischten Gas-Sattdampf Betrieb ergibt.

Während das P-V Diagramm einen glatten Kurvenverlauf aufweist, hat das entsprechende T-S Diagramm: "T2-S2" Abb.8 für den gemischten Gas-Sattdampf Betrieb "Peaks" und Überlappungen in den zwei Bereichen, wo die Entropieänderung das Vorzeichen wechselt. Abb.9.

Für ein zusammengesetztes Arbeitsfluid läßt sich nach meinem Kenntnisstand die mittlere Temperatur T2 nur mit der Entropie d_S2 folgendermaßen definieren:

(11.32) 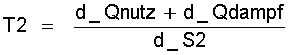     mit d_S2 = (d_S1 + d_S3)

d_Qnutz nach Gl.(7.2), Gl.(7.15) oder Gl.(8.10) und d_Qdampf nach Gl.(11.16). d_S1 nach Gl.(9.1) und d_S3 nach Gl.(11.18)

Die "Peaks" sind aufgrund der Null-Durchgänge in den Funktionen "d_Qnutz + d_Qdampf" = "d_Qnzd" und "d_S2" auch nicht anders zu erwarten. Dies geht sehr eindrucksvoll aus dem Diagramm "d_Qnzd" und "d_S2" als Funktion des Kurbelwinkels hervor; siehe Abb.9. Nach obiger Gl.(11.32) ist T2 = 0/0 bei Null-Durchgang von "d_Qnzd" und "d_S2", und damit unbestimmt.

Das Auseinanderdriften von T2 in Abb.8, bereits vor den Null-Durchgängen, sind aber grundsätzliche, keine numerischen Schwierigkeiten. Bei der Definition der Temperatur T2 ist dies geprüft worden, indem das Computerprogramm mit doppelter Genauigkeit gerechnet wurde !

T2 ist ja nicht unabhängig von S2 definiert wie die mittlere Temperatur "T" bei dem T-S1 Diagramm oder wie "T3" bei dem T3-S3 Diagramm:

• Für das T-S1 Diagramm (nur Gas) ist die Bezugstemperatur "T" nach dem idealen Gasgesetz definiert -siehe Gl.(6.1) oder Gl.(6.2), und

• für das T3-S3 Diagramm (nur Dampf) ist die Temperatur "T3" als Sattdampftemperatur definiert, die dem mittleren Dampfpartialdruck "Ps" Gl.(11.14) entspricht.

Die Entropien d_S1 bzw. d_S3 werden erst mit diesen Temperaturen errechnet -siehe oben- die GL.(9.1) und Gl.(11.18). Alle Werte für gesättigten Wasserdampf sind mit dem in |4| angegebenen -und von mir an einigen Stellen betr. FORTRAN 77 Syntax korrigiertem Computer Programm errechnet worden. Da diese Formeln dem neuesten Stand entsprechen und die genauesten Werte liefern, dürften die Überlappungen im T2 - S2 Diagramm also nicht die Folge ungenauer Werte für Verdampfungswärme, Dampfdruck, Sättigungstemperatur u.a. sein.

Waehlen Sie den Zurueck Schalter Ihres Browsers, um an die vorherige Textstellen zurueck zu kommen

Kapitel 10
weiter zu Kapitel 12

 Zurück zum Inhaltsverzeichnis