Dipl.-Ing. Peter Fette; Am Schäferloch 16; D-75045 Walzbachtal /Germany

 Zurück zum Inhaltsverzeichnis

Kapitel 14
weiter zu 16. Literaturnachweis

  15. Dynamische Bewegungsgleichung für die komplette Maschine

Im folgenden soll die Bewegungsgleichung für die komplette Maschine nach Abb.1 aufgestellt werden. Die bisher gebrauchten Bezeichnungen werden übernommen und Endziffern -von 1 bis 4- angehängt, um die jeweiligen Größen den Teilmaschinen zuordnen zu können. Die Indizes "I" bzw "II" deuten auf Größen in bezug auf die 1. bzw. 2. Kolbenstange hin. Reibungsverluste bei der Schwingungsbewegung der Arbeitsflüssigkeit werden mit berücksichtigt. Die Massen von Kolbenstange, Kolben und Arbeitsflüssigkeit sollen vereinfachend in der Flüssigkeitsmasse des jeweiligen "U-Rohres" zusammengefaßt sein.

• P i : Gesamtdruck, mit der Endziffer "i" von 1 - 4 für die jeweilige Teilmaschine   in Bar
• VE i : momentanes Expansionsvolumen                           in cm³
• DH    : Durchmesser des Expansionszylinders                  in cm
• HE i : Höhe des Gasraumes im Expansionszylinder          in cm
• VC i : momentanes Kompressionsvolumen                      in cm³
• DK    : Durchmesser des Kompressionszylinders             in cm
• HC i : Höhe des Gasraumes im Kompressionszylinder     in cm
• DKST : Durchmesser der Kolbenstange                           in cm

• MH : Masse in Gramm der Arbeitsflüssigkeit links und rechts vom Kolben in der U-Rohr Anordnung der "heißen" Zylinder.

  • MH_I ist dann die Arbeitsflüssigkeitsmasse für die Zylinder H1-H2 an der 1. Kolbenstange, die auf den Kurbeltrieb "KU1" wirkt und

  • MH_II ist die Flüssigkeitsmasse für die Zylinder H3-H4 an der 2. Kolbenstange, die auf den Kurbeltrieb "KU2" wirkt.

• MK : Masse in Gramm der Arbeitsflüssigkeit links und rechts vom Kolben in der U-Rohr Anordnung der "kalten" Zylinder.

  • MK_I ist dann die Arbeitsflüssigkeitsmasse für die Zylinder K4-K3 an der 1. Kolbenstange, die auf den Kurbeltrieb "KU1" wirkt und

  • MK_II ist die Flüssigkeitsmasse für die Zylinder K1-K2 an der 2. Kolbenstange, die auf den Kurbeltrieb "KU2" wirkt.

• ρ_W : ist die Dichte der Arbeitsflüssigkeit      in Gramm/Liter
• g ist die Erdbeschleunigung :          g = 981 cm / sec²
• P_U ist der Luftdruck der Umgebung. P_U = 1 Bar
• ω : ist die Winkelgeschwindigkeit ω = φ / d_t
• ω / d_t ist die Winkelbeschleunigung der Kurbelwelle
• φ = ω * t ist der Kurbelwinkel bezogen auf den Kurbeltrieb KU1
• "R" ist der Kurbelradius, der für beide Kurbeltriebe gleich groß ist     in cm

• WEG_I = R * (1 - cos(ω * t)) ist der Weg in cm des Kolbens der 1. Kolbenstange für einen Kurbeltrieb mit Kurbelschleife (siehe auch Gl.(2.6a); für einen Pleuelstangen Kurbeltrieb ist WEG_I entsprechend Gl.(2.6b) zu berechnen)

• U_I = d_WEG_I / d_t = R * ω * sin(ω * t) ist die Geschwindigkeit der 1. Kolbenstange     in cm/sec
• B_I = d_U_I / d_t = R * ω² * cos(ω * t)   ist die Beschleunigung der 1. Kolbenstange      in cm/sec²

• WEG_II = R * (1 - cos(ω * t - δ )) ist der Weg in cm des Kolbens der 2. Kolbenstange (siehe auch Gl.(2.7a); für einen Pleuelstangen Kurbeltrieb ist WEG_II entsprechend Gl.(2.7b) zu berechnen)

• U_II = d_WEG_II / d_t = R * ω * sin(ω * t - δ) ist die Geschwindigkeit der 2. Kolbenstange
• B_II = d_U_II / d_t = R * ω² * cos(ω * t - δ)     ist die Beschleunigung der 2. Kolbenstange
• Θ : ist das Trägheitsmoment der beiden Kurbeltrieben gemeinsamen Schwungscheibe      in Gramm * cm²

Um das Kolbenstangen Volumen berücksichtigen zu können, das in den Zylindern VE2 und VE4, sowie in VC1 und VC4 das Hubvolumen reduziert, werden folgende Querschnitte in den Flüssigkeitsräumen definiert:

• FQE = DH² * π / 4 , FQE nach Gl.(2.1.1) bei gleichem Durchmesser "DH" im gesamten U-Rohr für die heißen Zylinder;
• FQH = (DH² - DKST² ) * π / 4
• FQC = DK² * π / 4 auch hier bei gleichem Durchmesser "DK" im gesamten U-Rohr für die kalten Zylinder;
• FQK = (DK² - DKST²) * π / 4 . siehe auch Gl.(2.2.1);
• FKOL = DKST² * π / 4 ist der Querschnitt der Kolbenstange.

Die Gasräume in den einzelnen Zylindern sollen sich aus einem Totvolumenanteil mit der Höhe "H00E" und dem Regelvolumenanteil "RVE" mit der Höhe "HRVE" in den Expansionszylindern, bzw. dem Totvolumenanteil mit der Höhe "H00C", dem Regelvolumenanteil "RVC" mit der Höhe "HRVC" in den Kompressionszylindern zusammensetzen. Mit der momentanen Kolbenstellung WEG_I bzw. WEG_II ergeben sich die Höhen -in cm- der einzelnen Gasräume und deren Differentiale zu:

• HE1 = H00E + HRVE + WEG_I ,
• d_HE1 = d_WEG_I    ist das Differential von HE1.
• HE2 = H00E + HRVE + (2*R - WEG_I ) * FQH/FQE,
• d_HE2 = - d_WEG_I * FQH/FQE ist das Differential von HE2.
• HE3 = H00E + HRVE + WEG_II ,
• d_HE3 = d_WEG_II    ist das Differential von HE3.
• HE4 = H00E + HRVE + (2*R - WEG_II * FQH/FQE),
• d_HE4 = - d_WEG_II * FQH/FQE ist das Differential von HE4.
• HC1 = H00C + HRVC + WEG_II * FQK/FQC,
• d_HC1 = d_WEG_II * FQK/FQC ist das Differential von HC1.
• HC2 = H00C + HRVC + (2*R - WEG_II) ,
• d_HC2 = - d_WEG_II    ist das Differential von HC2.
• HC3 = H00C + HRVC + (2*R - WEG_I) ,
• d_HC3 = - d_WEG_I    ist das Differential von HC3.
• HC4 = H00C + HRVC + WEG_I * FQK/FQC ,
• d_HC4 = d_WEG_I * FQK/FQC ist das Differential von HC4.

Mit diesen Gasraumhöhen ergeben sich die einzelnen Volumina -in cm³- und deren Differentiale:

VE1 = FQE*HE1, d_VE1 = FQE*d_HE1; VC1 = FQC*HC1, d_VC1 = FQC*d_HC1

VE2 = FQE*HE2, d_VE2 = FQE*d_HE2; VC2 = FQC*HC2, d_VC2 = FQC*d_HC2

VE3 = FQE*HE3, d_VE3 = FQE*d_HE3; VC3 = FQC*HC3, d_VC3 = FQC*d_HC3

VE4 = FQE*HE4, d_VE4 = FQE*d_HE4; VC4 = FQC*HC4, d_VC4 = FQC*d_HC4

Die Druckunterschiede links und rechts der 4 Kolben bewirken die Bewegung der Kurbeltriebe. Dabei müssen die Flüssigkeitsmassen ( MH_I , MK_I , MH_II und MK_II ) sowie die Kolbenstangen und die Kolben selbst beschleunigt werden. Das Differential der Beschleunigungsarbeit z.B. der Masse MH_I inklusive der Kolbenmasse und anteiliger Kolbenstangenmasse ist:

MH_I * U_I * d_U _I

Die unterschiedlichen Höhen der Flüssigkeitssäulen bewirken Auf- und Abbau von potentieller Energie; z.B. bei den Säulen VE1 und VE2 ist das Differential der potentiellen Energie:

g * ρ _W * (VE1 * d_HE1 + VE2 * d_HE2)

Reibungskräfte an den Kolben- und Kolbenstangendichtungen, sowie Reibungskräfte in der Flüssigkeitsströmung wirken der Bewegung entgegen. Reibungsverluste in der Gasströmung durch den Regenerator bewirken einen Druckverlust, so daß man im Prinzip nicht von einem vollkommenen Druckausgleich in den Zylindern und Regenerator jeder Teilmaschine ausgehen kann. Bei kleinen Drehzahlen n < 300 U/Min sind die Druckverluste in der Gasströmung jedoch zu vernachlässigen und man wird bei der Berechnung dieser Maschine keine großen Fehler machen, wenn man von der Annahme eines vollkommenen Druckausgleichs ausgeht.

Die Reibungskraft "FSEAL" von je 2 Kolben und Kolbenstangendichtungen sei als konstant angenommen, da der Anpreßdruck der Dichtungen gegen die Zylinderwand bzw. gegen die Kolbenstange konstant ist. Der zu berücksichtigende Reibungskoeffizient wird -nach Start der Maschine von der Haftreibung in einen Mischreibungszustand- nur experimentell zu ermitteln sein. Das Differential der Arbeit dieser Reibungskräfte, die immer positiv anzusetzen sind, gehe für beide Kolbenstangen separiert in die Berechnung ein:

FSEAL * | d_WEG _I | + FSEAL * | d_WEG _II |

Um die Flüssigkeitsreibung mit einzubeziehen sei folgender Ansatz gemacht: Die Drehzahl der Maschine ist nur unwesentlich höher als die Eigenfrequenz der schwingenden Flüssigkeitssäulen in den U - Rohren, wenn man einmal den Kolben als reibungsfrei in der Flüssigkeit mitschwingend betrachtet. Diese Eigenfrequenz ergibt sich -unabhängig vom Rohrdurchmesser- aus der gesamten Länge " l_F " von Flüssigkeit + Kolben zu

(15.1)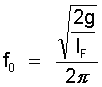

Die Kreisfrequenz ω sub 0 ist dann:

(15.2)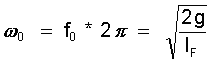

f₀ wird abgeleitet aus der Kräftebilanz an der frei schwingenden Flüssigkeitssäule. ("FQ" ist der Querschnitt dieser Flüssigkeitssäule. "X" ist die Schwingungsamplitude, "g" ist die Erdbeschleunigung)

(15.3) .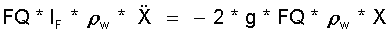

Daraus wird:

(15.4) .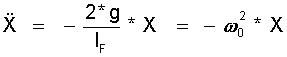

(15.5)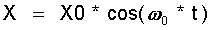

Zur Bestimmung der Länge l_F folgende Überlegung:

Bei der durch den Kurbeltrieb erzwungenen Schwingung beträgt die Schwingungsamplitude HE_min - HE_max = 2 * R ; R ist der Radius des Kurbeltriebs. Auch im unteren Totpunkt soll die Flüssigkeit noch oberhalb des U - Rohr Bogens bleiben; dann sollte auf jeder Seite des Kolbens mindestens eine Flüssigkeitssäule von der Länge 1/2 l_F ≈ 3 * R sein. Bezieht man noch die Flüssigkeitsmenge mit ein, die bei Teillast abgezogen und bei Vollast wieder eingespeist wird, dann sei l_F = 7 * R.

Die Flüssigkeitsreibung wirkt sich als Dämpfung einer freien Schwingung so aus, daß nach jeder Schwingung nur noch ein Bruchteil der vorigen Amplitude erreicht wird. Ein Teil der kinetischen Energie ist also in Reibungsarbeit umgesetzt worden. Die Verringerung der Amplitude kann gemessen werden: Faktor F_X = X1 / X0 . X0 ist die 1. Amplitude bei Start der freien Schwingung; X1 ist die Amplitude nach der 1. Schwingung. Bezieht man die geschwindigkeitsabhängige Dämpfungskraft mit in die Schwingungsgleichung Gl.(15.3) ein, dann erhält man:

(15.6)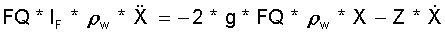

(15.7)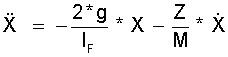

Mit FQ = Querschnitt, l_F = Länge und ρ_W der Dichte ist M = FQ * l_F * ρ_W die Masse der schwingenden Flüssigkeit. Z ist die Massengeschwindigkeit der Dämpfung. 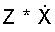ist die Dämpfungskraft, die mittels des gemessenen Amplitudenfaktors F_X = X1 / X0 berechnet werden soll: Aus Gl.(15.7) ergibt sich mit

(15.8)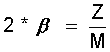

und der Kreisfrequenz ω₀ nach Gl.(15.2):

(15.9)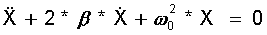

Lösung dieser Schwingungsgleichung mit Dämpfung ist:

(15.10)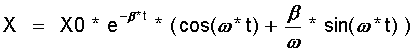

mit der neuen Kreisfrequenz

(15.11)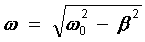

(15.12)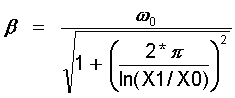

und die Massengeschwindigkeit Z errechnet sich über Gl.(15.8) und obiger Definition für β zu:

(15.13)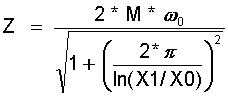

Die Dämpfungskraft 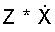aus GL.(15.6) wird mit der jetzt bekannten Massengeschwindigkeit Z -Gl.(15.13)- und mit den entsprechenden Flüssigkeitsmassen für jedes der 4 U-Rohre bestimmt. Die Geschwindigkeiten sind 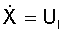bzw. 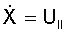. Da die Vorzeichen sowohl der Geschwindigkeiten U und die der zugehörigen Wegdifferentiale d_WEG immer gleich gerichtet sind, ergibt sich die Reibungsarbeit dieser Dämpfungskräfte für die beiden U-Rohre auf jeder Kolbenstange -immer als positiver Wert- zu:

(15.14)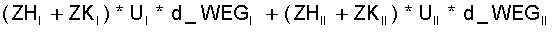

Wobei ZH_I , ZK_I , ZH_II , ZK_II gemäß Gl.(15.13) berechnet werden mit den jeweiligen Massen MH_I , MK_I , MH_II , MK_II in den einzelnen U-Rohren. Die Massen der Kolben und -anteilig- der Kolbenstangen sind, wie oben gesagt, in diesen Massen enthalten.

Nunmehr kann die dynamische Bewegungsgleichung für die ganze Maschine nach dem Energiesatz unter Berücksichtigung obiger Komponenten aufgestellt werden:

(15.15)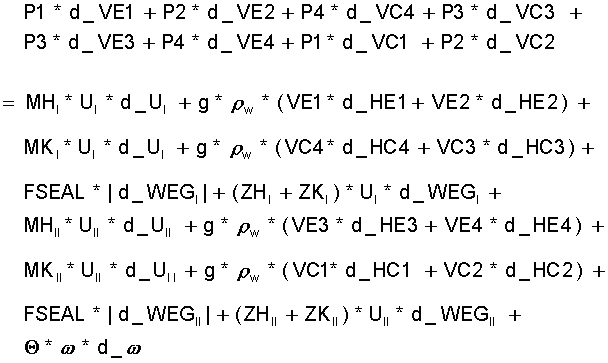

Setzt man in Gl.(15.15) die oben definierten Differentiale der Volumina und Gasraumhöhen ein, und setzt für d_U / d_t die Beschleunigung B, berücksichtigt ω = d_φ / d_t , und setzt für d_WEG / d_φ = U / ω dann kann man Gl.(15.15) nach d_ω / d_t auflösen und erhält: im - cm, Gramm, Sekunde, Bar - System (g=981 cm/sec):

(15.16)

Integriert man Gl.(15.16)   ∫ (d_ω/d_t) * d_t , dann erhält man die Winkelgeschwindigkeit ω und damit die Drehzahl "RPM" der Maschine.

Die einzelnen Elemente in den [ ] der Gl.(15.16) sind Kräfte. Der jeweils 1. Ausdruck in den beiden [ ] ist die Kolbenstangenkraft "SCHUB1" bzw "SCHUB2"; siehe Gl.(3.6) und Gl.(3.7). Alle anderen Kräfte in Gl.(15.16) werden als Verlustkräfte zusammengefaßt: VALL_I im Bereich der Kolbenstange 1 und VALL_II im Bereich der Kolbenstange 2. Die resultierenden Nutzkräfte auf den Kurbeltrieb sind dann aus Gl.(15.16) definiert zu:

(15.17)     FRES_I = SCHUB1 - VALL_I         bzw.

(15.18)     FRES_II = SCHUB2 - VALL_II.

Es läßt sich graphisch sehr anschaulich zeigen, wie mit steigender Drehzahl die Verluste zunehmen, wie die Nutzleistungskurve ein Maximum hat und die Drehzahlkurve später dann flacher wird, Abb.10. In diesem Diagramm wurde eine Maschine gerechnet mit einem Ausgangsdruck von P0 = 1 Bar. f₀ =0.84 Hertz. Andererseits -Abb.11- kann gezeigt werden, daß die Verluste klein sind, wenn bei höherem Ausgangsdruck -P0 ist hier 5 Bar- die Drehfrequenz w = RPM * 2 p / 60 der Maschine noch in der selben Größenordnung liegt wie die Eigenfrequenz f₀ = w₀ / 2 p der frei schwingenden Flüssigkeitssäule. Auch bei der Rechnung für Abb.11 ist f₀ = 0.84 Hertz. In diesen beiden Abb. sind über die Zeit aufgetragen: Alle Verlustkräfte "VALL_I" im Bereich der Kolbenstange 1, sowie die Drehzahl "RPM" und die Nutzleistung "POWERN" der ganzen Maschine. Die Nutzleistung "POWERN" ist jeweils während einer Umdrehung gemittelt, indem die während 1 Umdrehung verrichtete Nutzarbeit durch die Umdrehungszeit dividiert wird. So kann an der Länge der Horizontalen für "POWERN" auch gleich die Umdrehungszeit abgelesen werden, da die Abszisse die Zeit darstellt. Das Differential der Nutzarbeit aller Kolbenkräfte ist die momentane Nutzleistung. Diese errechnet sich aus den oben definierten Größen zu:

(15.19)     d_AKolN = ( FRES_I * U_I + FRES_II * U_II )

(15.20)    

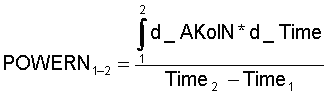
wobei Time₂ - Time₁ die Zeit für die 2. Umdrehung ist.

Man vergleiche die Drehzahl- und Nutzleistungs Kurven in den Abb.10 und Abb.11. In der Rechnung beider Diagramme wird zugrunde gelegt, daß keine Last abgenommen wird, so daß die ganze Nutzarbeit der Maschine in Rotationsenergie des Schwungrades umgesetzt wird. Man erkennt, daß die optimale Nutzleistung in einem Drehzahlbereich dicht bei der Drehzahl liegt, die der Eigenfrequenz der frei schwingenden Flüssigkeitssäulen entspricht. Dieses wird noch eimal deutlich bei der Gegenüberstellung der Drehmomentkurven mit und ohne Berücksichtigung der Reibungsverluste. So zeigt Abb.13 DREHMO die Drehmomentkurve ohne- , DRNUTZ die Drehmomentkurve mit Berücksichtigung der Reibungsverluste, POWERN ist wieder die mittlere Leistung, bezogen auf die jeweilige Umdrehung. RPM ist wieder die Drehzahlkurve.

Errechnet wurden die meisten Diagramme mit den folgenden allgemeinen Maschinendaten. Sie können auch mit der Demo Version des Programms STMOT2 nachgerechnet werden:

• Kolbendurchmesser in den H- und K-Zylindern = 10 cm sowie Kurbelradius R = 5 cm;
  Kolbenstangendurchmesser = 2 cm;

• Volumen in jedem Regenerator VR = 0.15 Liter;

• Ausgangsdruck P0 = 5 bar oder 1 bar; Ausgangstemperatur T0 = 300 Kelvin;

• Heiße Temperatur TE = 400 , kalte Temperatur TC = 300 Kelvin; Arbeitsgas: Luft, Arbeitsflüssigkeit: Wasser.

Alle Stoffwerte für Wasserdampf aus
     U. Grigull: NRB/NRBS Wasserdampf Tafeln. Springer 1988

     Ps Sättigungsdruck in Bar
     ρ Dichte in Gramm/Liter
     H Verdampfungswärme in Watt * sec/ Gramm
     S" Entropie des Dampfes in Watt * sec/(Gramm * Grd)
     S' Entropie des Wassers in Watt * sec/(Gramm * Grd)

Kapitel 14
weiter zu 16. Literaturnachweis

 Zurück zum Inhaltsverzeichnis