Dipl.-Ing. Peter Fette; Am Schäferloch 16; D-75045 Walzbachtal /Germany

 Zurück zum Inhaltsverzeichnis

Kapitel 8
weiter zu Kapitel 10

  9. Entropieberechnung zur Erstellung des T-S Diagramms

Mit der Definition von d_Qnutz nach Gl.(7.15) oder Gl.(8.10) kann jetzt die Entropieänderung des Gases in der Maschine berechnet werden:

(9.1)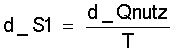

Die Integration bzw. die Aufsummierung von d_S1 zu S1 und die mittlere Temperatur "T" -siehe Gl.(6.1) oder Gl.(6.2)- ergeben das T-S1 Diagramm dieses isothermen Stirling - Prozesses mit Kurbeltrieb -Abb.6-, wobei der Bezugspunkt für diesen Kurvenzug frei gewählt wird. (Hier S₀ = 0 gesetzt.)

Die Entropierechnung für den idealen Stirlingprozeß erfolgt ebenfalls aus der Energiebilanzgleichung. Der ideale Prozeß kann ohne Hin- und Herschieben der Gasmassen in einem einzigen Raum erfolgen. Da die Gasmasse konstant ist, ist sie nicht mit in die Differentiation einzubeziehen. Die Energiebilanzgleichung wird damit einfacher. Statt Gleichung Gl.(7.2) oder Gl.(7.15) ergibt sich:

(9.2)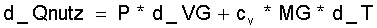

Das T-S Diagramm für den idealen Stirlingprozeß mit den gleichen Voluminagrenzen V_max und V_min wie beim Prozeß für die reale Maschine mit Kurbeltrieb ergibt, wie oben schon erwähnt, eine Art "Rahmen" um die Kurve, die sich aus der Entropieberechnung für den Prozeß in der realen Maschine mit Kurbeltrieb ergibt.
Die Kurve berührt den "Rahmen" bei V_min und bei V_max -entsprechend den Kurbelwinkelstellungen von 45 und 225 Grad; -diese Kurbelwinkelstellungen ergeben sich für den a-Typ Stirlingmotor bei gleichen Zylinderdurchmessern DH = DK.
Da das Regeneratorvolumen VR bzw. das gesamte Totvolumen in der realen Maschine immer > 0 ist, berührt die Kurve nicht die Isothermen TE und TC in Abb.6.

Das T-S Diagramm für den idealen Stirling Referenz-Prozeß -siehe Kapitel 5- hat die Form eines noch weiteren "Rahmens" wegen des größeren Volumenverhältnisses und wegen der größeren Temperaturdifferenz T_max - T_min .

Zur Berechnung des "Rahmens"

Ersetzt man "P" in der obigen Energiebilanzgleichung Gl.(9.2) nach dem idealen Gasgesetz durch P = MG * RG * T / VG , so ergibt sich die Energiebilanzgleichung zu:

(9.3)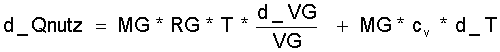

und die Entropieänderung ist:

(9.4)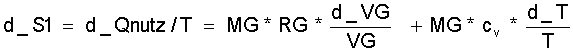

(9.4)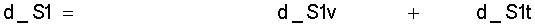

Da die Zustandsänderungen im idealen Stirlingprozeß nacheinander erfolgen, ist -wie oben schon gesagt- immer die gesamte Gasmasse MG beteiligt. Man unterscheidet wieder die isothermen und die isochoren Zustandsänderungen:

1) Entropieänderung während der isothermen Expansion bzw Kompression: Wegen T = const. gibt es keine Änderung der inneren Energie: Der Term aus Gl.(9.4) d_S1t = MG * c_v * d_T /T ist in diesem Bereich = 0.

(9.5)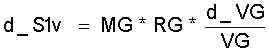

d_S1v kann sogleich integriert werden in den Grenzen von V_min bis V_max für die Expansion, und in den Grenzen von V_max bis V_min für die Kompression:

(9.5.1)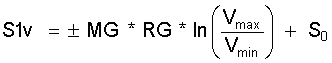

Die Werte "S1v" für die Expansion und "S1v" für die Kompression sind betragsmäßig gleich, unterscheiden sich aber wegen der Integrationsrichtung durch das Vorzeichen und erscheinen im Diagramm als horizontale Strecken gleicher Länge nämlich als die Isothermen TE und TC.

2) Entropieänderung während der isochoren Wärmezufuhr bei V_min bzw. während des isochoren Wärmeentzugs bei V_max: Da das Volumen während dieser Zustandsänderung konstant ist, gibt es hier keine Ausdehnungsarbeit: Der Term aus Gl.(9.4) d_S1v = MG * RG * d_VG/VG ist im Bereich der isochoren Zustandsänderung = 0.

(9.6)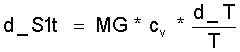

S1t muß schrittweise errechnet werden bei V_min für TC ≤ T ≤ TE bzw. bei V_max für TE ≥ T ≥ TC . Es ergeben sich leicht gekrümmte Linienzüge, die einander gleichen.

Der Bezugspunkt dieses "Rahmens" kann frei gewählt werden. Damit aber der Kurvenzug des realen T-S1 Diagramms zu dem T-S Diagramm-Rahmen des idealen Stirlingprozesses paßt, sollte der Bezugspunkt für den 1. Punkt des Kurvenzuges auch als Basis für die Berechnung des "Rahmens" gewählt werden. Wurde für S(1) = 0 gewählt, dann sind für diesen Punkt des Kurvenzuges die Temperatur T(1) und das Volumen VG(1) bekannt, und es kann von diesem 1. Punkt der Kurve zu dem 1. Punkt des "Rahmens" (z.B. dem Beginn der isochoren Wärmezufuhr S_Rahmen(1) bei V_min und T(1) = TC) zurückgerechnet werden.

Waehlen Sie den Zurueck Schalter Ihres Browsers, um an die vorherige Textstellen zurueck zu kommen

Kapitel 8
weiter zu Kapitel 10

 Zurück zum Inhaltsverzeichnis