Dipl.-Ing. Peter Fette; Am Schäferloch 16; D-75045 Walzbachtal /Germany

Zurück zum Inhaltsverzeichnis

8. Wärmeflüsse und Ausdehnungsarbeit bei verlustbehaftetem Regenerator

Bei einem verlustbehafteten Regenerator wird dem Gas auf seinem Weg vom Kompressionszylinder durch den Regenerator zum Expansionszylinder (Massenstrom d_ME > 0) im Mittel lediglich die Temperatur "TER" < TE aufgeprägt, und auf seinem Weg vom Expansionszylinder durch den Regenerator zum Kompressionszylinder (Massenstrom d_MC > 0) wird es im Mittel lediglich auf "TCR" > TC vorgekühlt.

Als wichtige Annahme zur Berechnung des isothermen Prozesses mit einem verlustbehafteten Regenerator sei hier statuiert, daß die Regeneratorverluste durch zusätzliches Beheizen des Gases im Expansionszylinder -siehe unten d_UREzu- bzw. durch zusätzzliches Abkühlen des Gases im Kompressionszylinder -siehe unten d_URCab- kompensiert werden müssen. Das hat zur Folge, daß die Nutzarbeit dieses Prozesses gleich ist der Nutzarbeit des Prozesses mit 100% wirkendem Regenerator.

Definiert man den Wirkungsgrad eines Regenerators zu:

(8.1) f8_1

als das Verhältnis der Temperaturdifferenzen, die das Gas jeweils beim Verlassen des Regenerators am heißen bzw. am kalten Ende erreichen wird (TER - TCR), zu der optimal möglichen Temperraturdifferenz (TE - TC) des Gases beim idealen Stirling Prozeß mit den Temperaturen TE und TC und mit idealem Regenerator, dann ist der Verlustfaktor beim Regenerator - Wärmeaustausch:

(8.2) RV = 1 - h_REG

Der Verlust sei jeweils auf das heiße bzw auf das kalte Ende bezogen. So ergeben sich die Temperaturen TER und TCR mit dem Verlustfaktor "RV" zu

(8.3) TER = TE - (TE - TC) * RV wenn d_ME > 0, sowie TER = TE wenn d_ME < 0 ist

(8.4) TCR = TC + (TE - TC) * RV wenn d_MC > 0, sowie TCR = TC wenn d_MC < 0 ist

Mit den in Kapitel 7 definierten Differentialen d_URE und d_URC ergibt sich die Änderung der inneren Energie bei der Wärmeübertragung in dem verlustbehafteten Regenerator analog zu den Gleichungen Gl.(7.13) und Gl.(7.14) zu:

(8.5) d_URE = c_v * (TER - TR) * d_ME

und

(8.6) d_URC = c_v * (TCR - TR) * d_MC

TR ist das log. Mittel der Temperatur im Regenerator, die hier analog zu Gl.(2.3) definiert wird zu:

(8.7) f8_7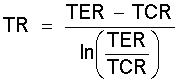

Der noch fehlende Energiebetrag zur Erwärmung des Gasmassenelementes d_ME auf seinem Weg vom Regenerator zum Expansionszylinder von der Temperatur TER auf TE:

(8.8) d_UREzu = c_v * (TE - TER) * d_ME

ist bei d_ME > 0 im Expansionszylinder nachzuheizen. Bei d_ME < 0 verläßt das Gasmassenelement den Expansionszylinder mit der Temperatur TE. Die Energie dieses Massenelementes d_ME geht in den Regenerator, um ihn wieder aufzuladen, so daß beim nächsten Gaswechsel im Mittel wieder die Temperatur TER erreicht werden kann, bzw. diese Energie muß bei einem verlustbehafteten Regenerator letztlich im Kompressionszylinder weggekühlt werden.

Der noch fehlende Energiebetrag zur Abkühlung des Gasmassenelementes d_MC von TCR auf TC:

(8.9) d_URCab = c_v * (TC - TCR) * d_MC

ist bei d_MC > 0 im Kompressionszylinder wegzukühlen. Bei d_MC < 0 verläßt das Gasmassenelement den Kompressionszylinder mit der Temperatur TC. Die Energie dieses Massenelementes d_MC geht in den Regenerator, um ihn ebenfalls wieder aufzuladen, damit das Gasmassenelement d_MC beim nächsten Gaswechsel in Richtung Kompressionszylinder wieder im Mittel auf TCR gekühlt werden kann, bzw. dieser Energiebetrag muß letztlich bei einem verlustbehafteten Regenerator im Expansionszylinder zusätzlich aufgebracht werden.

Mit allen bisher definierten Größen wird das Differential der Nutzenergie d_Qnutz aus Gl.(7.15) jetzt:

(8.10) d_Qnutz = P * d_VE + d_UTE + d_URE + d_UREzu

+ P * d_VC + d_UTC + d_URC + d_URCab

+ d_UTR

Betrachtet man die 3 verschiedenen Räume der Teilmaschine, den Expansionsraum, den Regenerator und den Expansionsraum in denen alle Zustandsänderungen, Energiezufuhr und Kühlung geschehen, dann ergibt sich d_Qnutz aus den Zustandsänderungen in diesen 3 Räumen auch zu:

(8.11) d_Qnutz = d_Qzu + d_Qab + d_UTR

Für den Expansionsraum definiert man die zuzuführende Energie:

(8.12) d_Qzu = P * d_VE + d_UTE + d_URE + d_UREzu

und für den Kompressionsraum definiert man die abzufährende Energie:

(8.13) d_Qab = P * d_VC + d_UTC + d_URC + d_URCab

Im Regenerator wird keine Ausdehnungsarbeit verrichtet, hier verändert sich nur die innere Energie UR -siehe Kapitel 7. Die Masse bezogene Ännderung der inneren Energie des Regenerators d_UMR siehe Gl.(7.12): d_UMR = - cv * TR * d_ME - cv * TR * d_MC ist bzgl. d_ME in d_URE aufgenommen worden und ist bzgl. d_MC in d_URC aufgenommen worden. Somit verbleibt aus d_UR nur noch der Anteil d_UTR -siehe Gl.(7.10), der noch zu d_Qnutz hinzuggerechnet werden muß. Gl(8.10) bzw. Gl(8.11).

Die Gl.(7.15) oder Gl.(8.10) ist die Grundgleichung nach dem 1. Hauptsatz der Thermodynamik zur Ermittlung des Verlaufs der Nutzenergie als Summe aller Energiebeiträge, die von außen und intern durch den Regenerator dem Kreisprozeß zugeführt werden, oder die ihm entzogen werden. Die einzelnen Energiebeiträge sind die Ausdehnungsarbeiten und die Änderungen der inneren Energie des Gases sowohl aufgrund der Temperaturänderungen in den jeweiligen Volumina der Maschine, wie auch die Änderungen der inneren Energie des Gases aufgrund der Massenänderungen bei den Gaswechselvorgängen. Mit d_UREzu und d_URCab in Gl.(8.10) können auch die Regeneratorverluste miteinbezogen werden. Wärmeleitungsverluste in den Zylinderwandungen, an den Kolbenstangen und an den Regeneratoren werden hier nicht betrachtet; zum einen, weil diese Verluste durch genügend gute Isolation klein gehalten werden können, zum andern sollen mit diesem Beitrag nur die wesentlichen thermodynamischen Zusammenhänge und Grundlagen des Prozesses und der Kinematik der Maschine erarbeitet werden.

Integriert man d_Qnutz über eine Umdrehung, dann erhält man die Nutzarbeit dieses Kreisprozesses. Festzuhalten ist, daß bei einem quasi isotherm ablaufenden Stirlingprozeß mit Kurbeltrieb und kontinuierlicher Kolbenbewegung die Elemente d_UTE, d_UTC und d_UTR entfallen -bzw. fast vernachlässigt werden können- , wohl aber müssen die Elemente d_URE und d_URC berücksichtigt werden; denn mit diesen Größen werden die in endlicher Zeit ablaufenden Gaswechselvorgänge berücksichtigt. Sie bedeuten hier die Änderung der inneren Energie des Gases, wenn es durch den Regenerator gedrückt wird. Bei 100 % wirkendem Regenerator heben sich im Verlauf einer Umdrehung d_URE und d_URC intern gegenseitig auf. Abb.4 zeigt, daß die Integration von d_URE zu QURE und d_URC zu QURC über eine Umdrehung = 0 wird. Abb.4a zeigt die Differentiale der Ausdehnungsarbeiten und der inneren Energie in den jeweiligen Volumina VE und VC.
d_URE und d_URC bewirken aber die Abrundungen, im Kurvenverlauf dieses Prozesses sowohl im P-V wie auch im T-S Diagramm, da diese Energieänderungen nicht ausschließlich und momentan bei V_max bzw. bei V_min erfolgen, sondern, wie oben schon gesagt, da sie eine gewisse Zeit benötigen und da sie dann wegen der kontinuierlichen Kolbenbewegung bei wechselnden Gasmassen in "VE" und "VC" stattfinden. In Abb.6 ist dieses besonders deutlich zu erkennen. Hier sind

das T-S Diagramm für den idelalen Stirlingprozeß (mit Regeneratorvolumen VR=0) und
das T-S Diagramm für den quasi isotherm verlaufenden Prozeß mit sinusförmig verlaufender Volumenänderung und einem realen Regeneratorvolumen VR > 0 sowie Totvolumina in VE und in VC dargestellt.

Beide Prozesse sind mit den gleichen Werten für V_max und V_min errechnet. Der "Rahmen" um die Kurve entspricht dem idealen Stirlingprozeß -siehe auch das in Kapitel 4 zur Arbeit "W" und " W_i " gesagte. Im idealen Stirlingprozeß entfallen die Elemente d_URE, d_URC und d_UTR, weil sich der ideale Stirlingprozeß in 1 Zylinder abspielen kann und theoretisch keine Gaswechselvorgänge nötig sind für die isochore Wärmeübertragung jeweils bei V_max und V_min . (Hier sind d_ME = 0 und d_MC = 0 siehe Gl.(8.5) und Gl.(8.6)). Im idealen Stirlingprozeß bewirkt der ideale Regenerator - ohne Volumen, VR= 0 daher auch d_UTR=0 - intern die isochoren Energiebeträge ± MG * c_v * (TE - TC)

Im idealen Stirlingprozeß wie auch im isotherm ablaufenden Stirlingprozeß mit Kurbelschleifentrieb und kontinuierlicher Verdrängersteuerung wird die Summe der zugeführten und entzogenen Energie vollständig in Arbeit umgesetzt, wenn der Regenerator 100 % arbeitet, d.h. wenn der Regenerator allein die in beiden Prozessen notwendige Änderung der inneren Energie bewirken kann. Allerdings ist die Nutzarbeit dieses isotherm ablaufenden Stirlingprozesses mit Kurbelschleifentrieb geringer. Dies zum einen, da wegen der kontinuierlichen und phasenversetzten Kolbenbewegung ein stetiger Gaswechsel zwischen Expansions- und Kompressionszylinder stattfindet, sodaß weder beim Expansions- noch beim Kompressionshub eine konstante Gasmasse in den jeweiligen Zylindern vorliegt (das ist der eine Teil der oben erwähnten Abrundungen im Kurvenverlauf im P-V und T-S Diagramm), zum andern, weil die im konstanten Regeneratorvolumen -bzw. Totvolumen- befindliche Gasmasse keine Ausdehnungsarbeit verrichten kann. Je kleiner das Regeneratorvolumen (Totvolumen) ist, um so mehr nähert sich der Kurvenverlauf den beiden Isothermen "TE" und "TC" und die Nutzarbeit des Prozesses würde größer.

Waehlen Sie den Zurueck Schalter Ihres Browsers, um an die vorherige Textstellen zurueck zu kommen

Kapitel 7
weiter zu Kapitel 9

Zurück zum Inhaltsverzeichnis