In the experiments, a large population of "genomes" (2,000-12,000) was used. Each genome initially consists of a functionally coupled pair of gene regulatory elements (O-gene + A-gene).

The "maternal" gradient of primary morphogen M (like bicoid or maternal HB) is predetermined. The exponentially decaying M-gradient activates the O-gene in a concentration dependent manner. In its turn, the O-product will also activate the A-gene in a concentration-dependent manner. (I take the Drosophila Kruppel gene as an analog of the O gene. According to figure 1, the HB gradient activates Kr in a concentration-dependent manner.) Concentration profiles of the O- and A-products for wild species have the following simple form shown in figure 4a and correspond to the early embryo phenotype with two bands of A-gene expression shown in figure 4b.

Figure 4a. The "maternal" gradient of primary morphogen M and the concentration profiles of the O- and A-gene products for wild species along the longitudinal axis of the embryo.
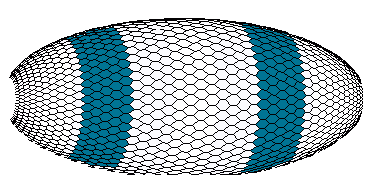
Figure 4b. View of the early Drosophila embryo with pattern of the A-gene product (computer graphics).
The wild-type genomes are two-string variables. The first (and odd-numbered) string has a fixed length of 3*(6+1)=21 symbols, while the second (and even-numbered) string has a length of 2*(6+1)=14 symbols. The A-gene string is CATAATnCATAATnCATAATn, where A, T, G, C is the four-letter DNA code and n is a spacer. The O-gene string has a similar form. A fixed probability for point mutations, that is for substitution of one of the symbols by another, is prescribed before the first run. When the computations begin, each genome is tested for "governing of development". This genotype to phenotype transformation is achieved by "translation" of the strings into coupled ordinary differential equations as follows:
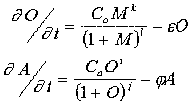
M is "maternal" morphogen. The constants C0, Ca, epsilon, and phi vary from 1 to 9 and can mutate by addition or subtraction of 1. k and i are equal to the number of active target sites in the string (2 or 3 for the wild genes O and A, correspondingly), while l and j are equal to the sum of the predetermined affinities of the target sites. As mentioned above, the O-product has an affinity not only to the unique CATAAT site but to the whole cataatfamily (see previous section). And each site of the family is characterised by its own affinity value. Weak, medium and strong affinity target sites for the morphogen M, O- and A-products are given.
The overall view of the eqs. set depends not only upon the number of gene-strings in a given genome, but also upon sequences of targeting sites. Special subroutine ('ODE_Set') analyses the sequences and choses equations of adequate structure (see next section).
After evaluation of the eqs. set the program finds the phenotype of the tested species. Namely, the values of the A-product (and products of other genes) are calculated for each of 50 points of the exponentially decaying M-gradient. The results are used for graphic presentation of the phenotypes and for the Scoring procedure.
The Scoring procedure compares the calculated set of the A-values with the prescribed canonical A-pattern. The sum of square deviations in each of 50 points of the M-gradient is calculated. If the sum is above threshold, then the species and its genome are eliminated. Only the form of the A-product gradient will be the target of stabilizing selection.
A few words concerning appearance of new genes may be in place. Mostly genes originate from duplication of existing genes. Any gene currently functioning in an organism will possess a backward genealogy to earlier, ancestral genes. The typical story for origin of any functioning gene includes: (i) sequence duplication; (ii) fixation in the population, through selection or drift; (iii) maintenance of function by selection; and (iv) sequence evolution under mutation and selection (see Altenberg, 1995):
1. Thus functionally successful duplication yields apart from a given gene pair, their extra-copies O' + A'. Duplications in the model are represented by adding of pair of new strings to the given genome. If initially all species have two-string genomes, at the end most of the species have six-string (six-gene) genomes.
2 At first, on the evolutionary time scale, this pair obviously is silent because of evident functional uselessness. As a result, in offspring genomes the O' + A' genes have the freedom to accumulate point mutations.
3. During this period, the key event is an appropriate mutation in the coding part of the O' gene (probably in the part coding DNA-binding domain) which changes DNA recognition specificity. (It was apparently a slight change, so that 2 or 3 nucleotides substituted in the consensus sequence.) As a result, a "fortunate" O' gene will get a chance to become a B-gene in a growing cascade. Which features or mechanisms are needed for evolutionary change of DNA-protein recognition specificity is a very complicated question. The idea of a DNA-recognition code for transcription factors is attractive (Suzuki & Yagi, 1994; 1995; Choo & Klug, 1994a, b). As a first approximation we could assume such a self-evident fact as that the initial change of the recognition specificity is a slight alteration of the consensus sequence of sites being recognised. This simple assumption agrees with the scheme of one to one interaction between amino acids and bases in zinc-finger recognition of DNA (Choo and Klug, 1994a; b). This basic assumption is sufficient to enable us to follow the cascade of down-growth via duplications. (The same is true for the A').
4. For the purpose of an oversimplified but indirect implementation of the driving force, I assume the appearance of a "virus". The virus is randomly transmitted from "carriers" to healthy genomes. By definition, the virus is successfully transmitted if the host genome has in the A-gene an O-binding site. I assume it inserts in the A-gene by cutting of the O-binding site and becomes silent. With a predetermined probability the virus wakes up and with time gradually decreases the host's reproductive potential, finally killing the host, thus eliminating the affected genome from evolution.
Point mutations in the O-binding sites lead to insensitivity to virus. However, the "wild" type of our genome could not lack the O-binding sites in A-gene, because it would consequently lack the normal phenotype (the A-product concentration profile). Hence, in the case of a genome with absence of the wild-type O-binding site in the A-gene (but with a normal pattern of A-gene expression), this prospective mutant will be insensitive to the virus and obtain a selective advantage. In time, the mutant genome will exclude the wild type. This is, of course, a model example of host-parasite evolution.
I must emphasize that such selection by parasite pressure is effective only if the design of the wild genome allows appropriate reorganization in principle. The virus acts as a catalyst of the process. It does not produce but catches new forms. If the wild-type genome does not have an appropriate potential for reorganization (testable in calculations), a virus will not help. In this I imply a broad interpretation of "virus", that is, it may be plasmid or another genome element. I also assume that the virus sequence specificity can mutate (with very low predetermined probability). As a result the mutant virus can find and insert in other site than the wild-type O-binding one. But the mutant still can insert only in the A-gene or its extra-copies and offspring genes.