If the fitness landscape is flat, as is the case of neutral evolution, the population will wander at random through sequence space. If the landscape is not flat then selection will tend to drag the population towards regions of higher than average fitness. In our computations we find three attractors in our fitness landscape. The first "hill" corresponds to the wild type genome, the second "hill" grows owing to the four-gene cascade, and third hill's appearance is conditioned by the six-gene cascade. In conditions of moderate pressure by the "parasite", we can simultaneously observe all three examples in a computed population (figure 5).
If we exclude virus from the computational evolution, then there is still a vanishing but still defined probability for appearance of 4-gene species. When we treat large populations (12,000) without the virus pressure, we sometimes fix appearance of unique genomes with functional four-gene cascades. They appear via a random walk owing to the absence of selective disadvantages for 4-gene cascades compared to wild-type genomes. The mere fact that we treat DNA-like sequences, permits us to use common software for the nucleic sequence analysis. Figure 10 shows the results of a phylogenetic analysis of genome sequences collected in the course of one of our computations.
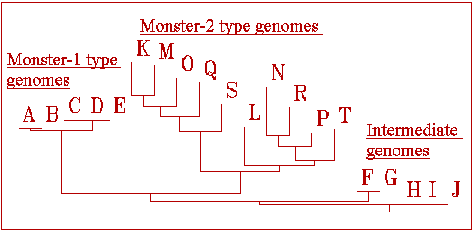
Figure 10. Dendrogram calculated by the software package CLASTAL (Higgins & Gibson, 1994) for a "collection" of genomic sequences gathered at the stationary phase of our computations (as at the upper part of the scheme in figure 5). Genome sequences are named for convenience by one-letter names.
The resulting phylogenetic tree vividly reminds us of many known examples of dendrograms of real families of biological macromolecules! (In the case of the figure 10, we treat only relatively large genomes with four- and six-gene cascades, which gives better statistics). Our computations reveal simple but impressive examples of rising structural and functional redundancy in an evolutionary computation:
0 -> A
0 -| A
The pair of wild-type genes O + A and the six-gene cascade really perform the same task: maintenance of a two-wave pattern of A-gene expression. Such enormous redundancy is ensured by known features of kinetics of gene expression (as discussed in section 2). Formally, evolutionary growth of the gene net corresponds in the model to step-by-step increments of the size of the ODE set describing the genotype to phenotype transformation. If initially we have a generalized Hill-type equation, as mentioned in Section 4, then finally we obtain an ODE set containing five equations (for the dynamics of expression of the A, B, C, D and E genes):
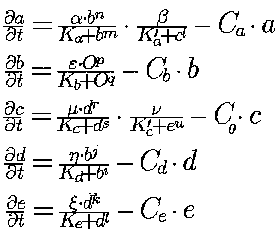
where Greek letters and indices K's and C's are parameters.
Such increasing redundancy one might regard as a trick, but this computer trick could resemble the macroevolutionary appearance of the enormously complicated gene mechanisms for early Drosophila segmentation. Once upon time, such structural/functional redundancy could have been taken up by Nature for raising of organization level of its creatures.