Although a large literature exists for equations which specify fields of values in the plane with specified boundary values, or sphere, little or no literature exists for the case where the "morphogen field" interacts with the surface to change its shape, and the field in turn is itself changed because of the changed surface, and so on (but see Cummings, 1985; 1989; 1990; 1994; Spirov and Boinovich, 1985; Spirov, 1992; 1993a,b). Change of shape could of course involve aspects of mechanical forces just as important as the chemical-kinetics aspects, and equally deserving of inclusion in the differential equations. However, in the pattern-form interplay models we explore the possibility that the secondary role of mechanics can be represented algorithmically (Cummings, 1985; 1989; 1990; 1994; Spirov, 1992; 1993a,b; Harrison and Kolar, 1988). Certainly, the present model of morphogenesis is capable at best of providing only an insight into such a complex process, and only on the highest scale, that of the cell collective.
All Turing-like models require two diffusing substances as a minimum,
one [X] comparatively slow-diffusing one and a second [Y] that is much
faster (Lacalli & Harrison, 1991). All 2-morphogen models require X-autocatalysis
and cross-inhibition via a second species, Y. The Y can be inhibited or
depleted by X formation but activates the latter, as in the Brusselator.
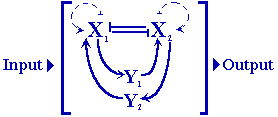Symmetric 4-morphogen
systems (with paired Xs and Ys, as in the case of dual Brusselator) belong
to models with the general attributes of mutually exclusive states for
production of each of two self-activating morphogens that are cross-activating
via two further, faster diffusing morphogens.
We use here, following other authors (Harrison, Kolar, 1988; Harrison et al., 1988), the Brusselator as a system that has been extensively studied in relation to chemical pattern formation as well as dual Brusselator as system with perfect interpretation in molecular biology terms (Lacalli, 1990). Namely, assuming the morphogens involved in gradient formation are primary gene products and not metabolites, the main steps in the reaction scheme leading to X and Y formation must represent some combination of gene transcription processes. This, in itself, implies considerable complexity and regulatory control. The model specifically requires there be multiple inputs, including some type of the gene self-activation by products (Lacalli, 1990).
We consider the application of these ideas to the object-oriented modeling of specific morphogenetic processes such as gastrulation of sea urchins. Initially the model describes geometry of a spherical layer. The program considers each of about 1000 cells as CELL-object with known space co-ordinates of 6+6 apexes and local concentrations of Xs and Ys. LIST of all CELL-objects is used for generation of new object "GASTRULA". (Then procedure MOVE.TO change local cell co-ordinates of the GASTRULA according to local Xs concentrations.) Each cell produces and exchanges the morphogens X(s) and Y(s) in conformity with Brusselator or dual Brusselator model. The set of parabolic equations is solved by the finite difference method.
A predominant animal-vegetal polarity axis of the zygote is reflected in the model by appropriate boundary conditions: fixed concentration of the morphogen(s) X(s) on the vegetal pole and zero concentration on the animal pole. Thus first circle of animal cells of the model corresponds to secondary mesenchyme of echinoderms blastula. Under certain initial conductivity of cell-to-cell communications the trivial homogeneous distribution of morphogens is unstable.
Steps in computation of the morphogen distribution must be altered with steps in which the new morphogen distribution is used to govern morphogenetic movements. On first and following odd numbered steps, numerical integration of the equations was carried out until a steady state was reached. On second and following even numbered steps, "translation" of new patterns into new forms occurs by means of "morphogenetic movements". This is yet another feedback loop. The reaction-diffusion prepattern must be continually reorganizing itself in response to the change of shape of the simulated object, which in turn is occurring because of the existence of the prepattern (Cf. Harrison and Kolar, 1988).
Morphogen-induced morphogenetic movements are somewhat separated in time according to the model. It is to be noticed that the morphogen pattern develops first, followed by the appropriate morphogenetic movement (geometric change). This feedback loop from the patterns of morphogens to changes of surface geometry is determined by X-concentration dependent cell form changes (namely columnarization of cells and/or cell apex constriction). The particular examples of elementary cell shape transformations are shown in Fig.2.
FIG.2. The variation of shape of cells with morphogen concentration for the case of symmetric distortion. "S" is the ratio of local basal to apical cell surface area, and "h" is the local sheet thickness. The height "h" is assumed to stay constant in this figure. (According to Cummings, 1994).
According to Amemiya (1989), invagination begins via apex constriction of initial cells at the blastula vegetal pole. As a result, neighboring cells were initially pulled toward the first cells by their contraction. The neighboring cells appeared to respond to the stretch by their own apex constriction. This pulled the next group of adjacent cells. This wave of apical constriction was thus spread from the vegetal pole radiating outward. .
Fred Cummings (1989; 1990; 1994) have been studied elementary expressions for the gauss curvature K in terms of the parameters s, the ratio of local basal to apical cell surface area, and h, the local sheet thickness. The sheet thickness and the basal to apical ratios will be presumed to be a slowly changing function of cell position.
FIG.3. A cross-section through the cellular monolayer along one principal direction in the surface.
Pictured in Fig.3 is a section of the sheet, indicating a gradual change in both h and s as we move to the right of the picture. The apical area is indicated as "a" in the figure, and the basal area as "b". Also shown are the three radii R(a,1), R(b,1), and R(1); R(a,1) and R(b,1) are the radii of curvature of the apical and basal areas respectively, in the "one" direction, and R(1) is the corresponding radius of curvature of the middle surface, which is shown as a dashed line. What is not shown are the corresponding quantities in the orthogonal direction (into the page), that is, the R(a,2), R(b,2), and R(2).
The problem at hand is to relate the radii of curvature to s and h, and thus to K, which is related to R(1) and R(2) by K = 1/ (R1*R2).
Elementary solution this exercise, according to Cummings, gives
.
Thus, empirical knowledge of the dependence of s and h on the morphogen m will determine the gauss curvature at each point on the surface. It seems reasonable to presume, for example (Cummings, 1994), that both of these functions s(m) and h(m) are monotone functions of m, perhaps even the "S" shaped functions so familiar to biological mechanisms. The MOVE.TO procedure of the model uses such "S" shaped functions for s(m) and h(m).
Get your own Free Homepage