3. THE CHANGE OF INITIAL SYMMETRY IN MORPHOGENESIS SIMULATION
Carrying out a number of computer experiments with the model reveals behavior similar to early stages of sea urchin morphogenesis. The model simulate flattening of a blastula bottom, invagination, elongation and since then a morphological metamerization ("chambering") of a "gut" with maintenance of an initial axial symmetry (an animal-vegetal axis) as well as determination and invagination of an "orus" (i.e. determination of a second axis of symmetry: an oral-aboral axis).
There are such modes of the model behavior as invagination followed by elongation and then a morphological metamerization of a "gut" with maintenance of an initial axial symmetry (1); invagination followed by formation of bilaterally symmetrical "pockets" on the initial invagination , i.e. replacement of axial by bilateral symmetry (2); and lastly invagination followed by determination and invagination of an "orus", i.e. with determination of a second axis of symmetry (3). All three developmental pathways are described in (Spirov, 1993). In case (1) there occurs a secondary bifurcation from a simple gradient, described by spherical harmonics Y(11), to the pattern, described by spherical harmonics Y(lm) with a non-zero value of order m (Fig.4).
A. 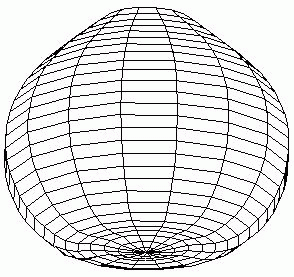
B. 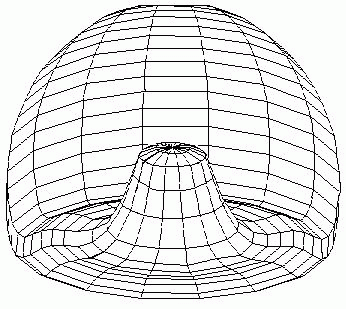
C. 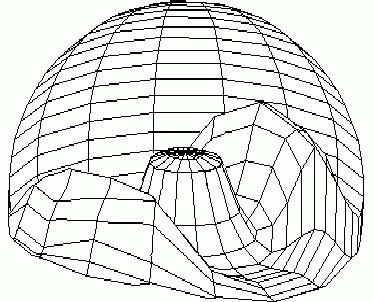
FIG.4. First scenario of the pattern-form interplay in the model of sea urchin early development with change of initial axial symmetry into bilateral (Spirov, 1993a).
In case (2) the series the morphogen patterns are formally described by spherical harmonics of general form Y(l0) with zero order parameter, i.e. the processes in the model maintain axial symmetry. A third series demonstrates determination of the second axis of symmetry and the invagination not only a "gut", but also an "orus" in the model embryo (Fig.5).





FIG.5. Third scenario of the dynamics of pattern-form interaction with change of initial axial symmetry into biaxial (Spirov, 1994).
Axel Hunding (1987) has been numerically and analytically investigating secondary bifurcation points for spherical reaction-diffusion system, when initial symmetry is broken by making diffusion- and rate-coefficients functions of primary gradient. His results that the emergence of the perpendicularly oriented bipolar pattern obtains a broad class of chemical reaction systems are an important result in the context of early holoblastic egg development. It explains emergence of a bipolar order orthogonal to the animal-vegetal axis in the early sea urchin blastula. Our tilting of initial animal-vegetal gradient to secondary Oral-Aboral axis for axially symmetrical closed layer reminds recent results of (Hunding, 1987; Hunding and Brons, 1990).
In toto, the dynamics of (bio)chemical pattern observed in our computer experiments and its connection with the morphogenetic movements is in close agreement both with classical works of Child (1936) about physiological gradients in echinoderms development (Cf. Our Fig.4 with Fig.1). As well as with modern investigations on region-specific gene expression prior and at gastrulation in sea urchin embryo (Wilt, 1987; Davidson, 1989; Livingston, Wilt, 1990).