Turing Systems
Brusselator
Each "cell" produces and exchanges the morphogens X and Y in conformity with Brusselator model. The set of parabolic equations is solved by the finite difference method in accordance with the scheme:
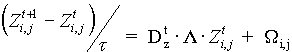 , (1)
, (1)
where
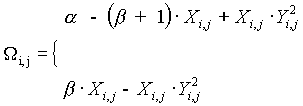 , (2)
, (2)
and
![]() , (3)
, (3)
![]() is a concentration of
the morphogen X or Y in the cell from i-circle and
j-row of the grid at the moment t, while
is a concentration of
the morphogen X or Y in the cell from i-circle and
j-row of the grid at the moment t, while ![]() is the concentration at a moment t+1;
is the concentration at a moment t+1; ![]() is a transport coefficient for the Z-morphogen at the moment t;
is a transport coefficient for the Z-morphogen at the moment t;
![]() are the right parts of Brusselator
kinetic equations in dimensionless form;
are the right parts of Brusselator
kinetic equations in dimensionless form; ![]() and
and ![]() are parameters;
are parameters; ![]() are transport members which describe the intercellular exchange of the
X or the Y morphogens at the moment t;
are transport members which describe the intercellular exchange of the
X or the Y morphogens at the moment t; ![]() is the morphogen concentration in the right neighbor cell,
is the morphogen concentration in the right neighbor cell, ![]() is in the left neighbor cell, while
is in the left neighbor cell, while ![]() is in the upper and
is in the upper and ![]() is
in the lower neighbor cell. The time increment is
is
in the lower neighbor cell. The time increment is ![]() =
0.01;
=
0.01; ![]() and
and ![]() are space increments;
are space increments; ![]() and
and
![]() are spatial coordinates
along the surface in two directions (polar coordinates).
are spatial coordinates
along the surface in two directions (polar coordinates).
This is two examples of stable patterns observed in case of Brusselator Reaction-Diffusion System for spherical surface (waved and patched patterns). The more blue 'nucleus' inside a cell the more local concentration of one of the Brusselator intermediates [X].

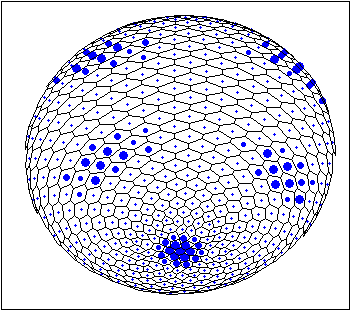
For details See:
Fromherz model: self-organization in the system of ionic channels in biomembranes
According to this model, electrically charged channels in a fluid membrane may form dissipative structures driven by a concentration gradient of salt. On a molecular level the effect is due to dissipative attractive forces; the channel currents induce local gradients of the membrane potential that interact with the protein charge. The ion flow through each channel induces a halo of lateral current and a radial gradient of electric potential. Other channels are attracted if the sign of the charges is matched to the polarity of the ion current. Around a transient cluster, however, the gradients are superposed such that drift may overcome Brownian motion. As a result, a macroscopic pattern may arise from the fluctuation. This self-organization by charged channel condensation is treated by a coupled system of equations: Smoluchowski's equation describing diffusion and drift of the membrane channels (dynamics of the channel density N) and Kelvin's equation describing the dynamics of the membrane potential V.
Equations of the model describe dynamics of the membrane electric potential
V and of the ionic channel density N on the membrane surface
(in dimensionless variables):
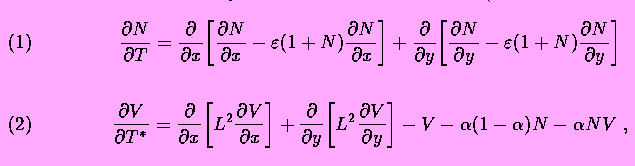
where x and y are space coordinates, ![]() ;
;
![]() and L are parameters,
and L are parameters, ![]() with
with ![]() ,
, ![]() being time intervals, and t is the physical time.
being time intervals, and t is the physical time.
This is example of polyfocal stable solution. Potential V local values is portrayed by blue palette.

For citations and details See "Electrically
Active Cell" Pages
![]()
![]()
![]()
This page hosted by ![]() Get your own Free Homepage
Get your own Free Homepage