According to Fred Cummings (1985) the Helmholtz algorithm for regulative patterning has following formulation: At each time frame each interior square has a value which is slightly greater then the average value of the nearest neighbors at the preceding time step.
This definition embraces a vast of models. Their Helmholtz-like equations
has often been invoked in the past in the context of developmental patterns
(Kauffman et al., 1978; Kauffman, 1993; Trainor and Goodwin, 1980; Hunding,
1981; Lacalli and West, 1986; Murray, 1981; McNally and Cox, 1989).
Below two figures that illustrate scaling invariance for following Helmholtz-like equation:
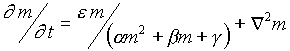
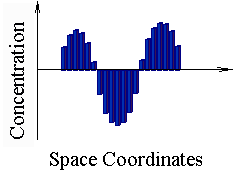
It is stationary states for 25- and 75-cell length one-dimensional solutions.

The model can most easily be introduced via a one-dimensional schematic (figure). Figure considers a linear array of cells connected by adhesion molecules, which molecules come in two types, "red" and "blue", and are perhaps conformational forms of the same molecule. In the more general case of a two-dimensional surface, the molecules will connect the cells in these epithelial sheets by their lateral surfaces. The molecules distribute themselves according to the following simple rules.
First, in the absence of interaction between red (R) and blue (B), each, R and B, will distribute themselves as smoothly as possible over the surface (in the case of the Figure, over the length) consistent with boundary conditions. These "smoothing" propensities of the two molecules has been noted often before as a common theme in patterning mechanisms, and may be viewed as a generalisation of the French, Bryant and Bryant (1976) rule of shortest distance interaction, when gradients are minimised (see also Kauffman, 1993). It will be assumed that there is an energy "cost" to maintaining of either type, red or blue, so that the overall energy is minimised by lowering gradients.
The second rule is that the R and B interact, and this effective repulsive interaction causes them to avoid each other; they "repel" each other. Presence of a high concentration of R tends either to cause B to (autocatalytically) convert to R, or else for B to migrate in the membrane to regions of lower concentrations of R, and vice versa.
The lowest energy configuration will be sought such that these two rules are obeyed. It will result from these two rules that the (weighted) sum of the concentrations of R and B satisfy the well known Laplace equation; in one dimension this is a simple linear gradient. Thus as seen in Figure, the total of R equals the total number of B, and each cell has the same total of R + B, when the solution to Laplace is a constant. The constant solution for Laplace is the absolute minimum of energy, and the situation when squared gradient of the sum of R and B is zero.
Very complex patterns arise from this simple algorithm on the surface of interest, and it yields many of the same steady state patterns as the Reaction-Diffusion models, although the conceptual basis here is very different.
Part of the present motivation is the striking fact that if one takes a small piece from the length of a hydra, the small piece will reform itself into a miniature hydra by reforming the head (or foot) at its original end. Hence it remembers the direction of the original gradient from the small trace gradient remaining just after excision, suggestive of such a process as outlined above. Hydra will accomplish this regeneration down to excised pieces as small as five percent of the original body mass (Bode & Bode, 1984).
The original density of R is re-established at the "head"
end in the excised piece; since energically speaking, R avoids B, and since
a given cell has a fixed sum of R and B, then R will collect at the head
end, and B at the other in the excised piece in the simplest one-dimensional
example, since this is the lowest energy configuration, as will be seen
below. It seems simpler to conceptualise this feat of regeneration (and
the regeneration of "high" and "low" positional values
in the shorter hydra) from the present point of view than from the point
of view of RD schemes.