The startling and much repeated observation first made by Driesch in 1891 that any of the meridianal blastomeres of 2-cell or 4-cell sea urchin embryos are capable of forming a complete embryo if cultured in isolation (reviewed by Horstadius, 1973, pp.92-99). One of modern attempts to explain this scaling invariance is Belintsev & Beloussov model.
The deformation of the bottom of blastula via archenteron invagination is preceded by the establishment of specific morphological patterns in the initially homogeneous cell sheet. This pattern is first visualised as domain of polarised (apico-basally elongated) cells gradually delimiting themselves from the surrounding tangentially stretched cells. This domain later becomes the area of extensive active epithelial deformations (morphogenesis).
Polarisation of embryonic cells is an active process that accompanying by profound transformation of the cytockeleton-associated intracellular structures (Belintsev et al, 1987).
The morphometrical measures of cell polarisation in the epithelial sheets have led to the "all-or-none" conclusion in the character of the process (Petrov & Beloussov, 1984).
The non-triviality of cell morphological polarisation may be derived from the fact that a capacity for it is associated with define and limited periods of development (Petrov & Beloussov, 1984). At the same time, the number of embryonic cells possessing this capacity is much greater than that being actually polarised in normal development. In sea-urchin embryo at the blastula-early gastrula stages (Beloussov & Bogdanovsky, 1980) practically all the cells are capable of being polarised after dissections. Normally, however, this capacity is expressed only in the late blastula vegetal plate.
The above-presented review of experimental data may be summarised as follows:
(1) Individual cells of morphogenetically active embryonic epithelia are mechanically active. They can deform themselves to acquire one of two discrete shapes isodiametric or elongated normal to a layer surface, both being stable against small perturbations.
(2) The cell material of an epithelial tissue considered as a solid medium posses passive elasticity in a purely mechanical sense.
(3) The mechanical activity of a given cell is modified by contact influences exerted by adjacent cells. The contact interactions provide for the short-range co-operativity of cell polarisation.
(4) Elastic stresses in epithelium interfere with mechanochemical activity. For instance, lateral transitions suppress cell polarisation normal to the cell sheet surface.
According to Belintsev model, sea urchin blastula is considered as a spherical monolayer of cells. The cells are attached to an elastic substrate and joined to one another. Each cell is simulated as an elastic unit in the isotropic relaxed state. In addition. the cells are considered as mechanically active elements which posses an alternative stable state with morphologically polarised (columnar) shape. Apparently the elongation of a cell involves work performed against elastic forces. In contrast, only the passive elastic forces can arise in the substrate.
Belintsev phenomenological model does not assume any particular mechanism responsible for the active cell deformation (Cf. Gordon, 1993). Instead, a scalar phenomenological parameter P is introduced. By assumption P equals zero if the mechanochemical activity is switched off. When this activity makes the cell elongate normal to the sheet plane, one ascribe to it p>0.
Based on this general definition, the observed features of the cell
polarisation process may be rewritten as a kinetic eqn.:
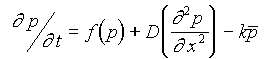
Here the spatial distribution of the cell activity within the sheet is approximated by the continuous two-dimensional field of parameter p. The first term of the eq. presents the self-regulated character of the mechanochemical activity; the second term - its transition between adjacent cells and the third term - its modulation by lateral stress in the sheet.
The fact that one can observe two distinct classes of cell morphology
allows one to assume the trigger-like control of the cell activity. One
can simulate this by the N-like shape of the
function f(p): ![]()
The operator delta in the eqn. does not necessary imply the diffusion of some intermediates. This kind of operator emerges as a first approximation when considering the short-range interactions which result in the co-operativity of cell behaviour.
The third term in eqn. represents the effect of external forces applied
at the lateral cell margins.
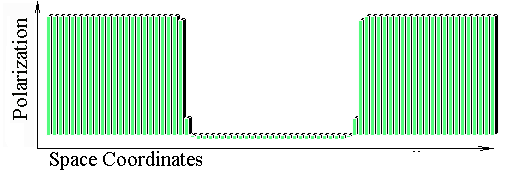
The Belintsev equation was treated as PC-simulation. Following two figures present steady patterns of cell polarization states for the one-dimensional case. In these cases polarization p initially induced in end-cells. In the first figure we have 30-cell row, while in the second figure we have 90-cell row. These pictures illustrate perfect scaling invariance for the model.