A vast word of regulative models comes to light in the field of epithelial
morphogenesis. Fred Cummings, simply starting from the extremum formulation
of the Laplace algorithm for the multicellular layer morphogenesis (as
in the case of Fig.#) with a necessary constraint, was lead to following
non-linear equation for morphogenesis. In conformal co-ordinates u
and v this equation has form:
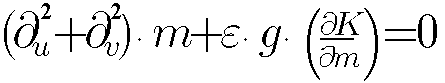, where K is Gauss
curvature of the epithelial layer, m is local morphogen concentration,
g is metric function and e is parameter. The
term 
act as a self-source
term in this Poisson-like equation. This interesting equation turned to
exhibit size invariance as a very natural consequence, almost as a sort
of side benefit, and not as a contrived effect. As Cummings (1990) wrote,
it is apparent that it will be difficult to think of another way in which
the size invariance could occur.
Equally with self-organisation via pattern-form interplay (Game of Morphogenesis),
the size regulation is considered as a fundamental aspect of biological
morphogenesis. Algorithms of the regulative morphogenesis, elaborated in
theoretical biology, must have perspectives for application in the field
of artificial morphogenesis, in ALife.
Get your own Free Homepage