What Can We Learn from the Pattern-Form Interplay Models?
Alexander V. Spirov
Institute of High Performance Computing and Data Bases
Sechenov Institute of Evolutionary Physiology & Biochemistry; S.-Petersburg; RussiaAbstract
We treat the problem of how the information encoded in linear DNA molecule becomes translated into a three-dimensional form from position of Pattern-Form Interplay Models. The characteristic feature of these models is an existence of feedback loop from (bio)chemical pattern formation to modelling embryo form changes. In accordance with the model the system is open and changes in a pattern give rise to changes in form and these changes in form (surface geometry) cause further pattern changes, and so on.
Spontaneous pattern formation takes place in the model as primary and secondary bifurcations of non-linear parabolic PDEs describing reaction-diffusion systems with imposed gradient. We briefly review the main results of previous work and consider new phenomenon of axis tilting as the case of symmetry breaking via secondary bifurcations. The axis tilting bifurcation occurs as a consequence of position-dependency of diffusion coefficients. The explicit demonstration of this phenomenon in Pattern-Form Interplay Models is believed to be new.
1. Introduction
One of the most intriguing problems facing modern science is to understand the genesis of organismic form. The question of how the information encoded in linear DNA molecule becomes translated into a three-dimensional form has to date no satisfactory answer. We follow the point of view of Frederick Cummings [1994] who proposed to ask "How do we imagine it could have happened?", rather then "How did it happen?". We share an assumption that a common strategy was evolved for the formation of multicellular organisms, which can be described as a set of generative rules or algorithms. These rules are reasonably simple when considered on a certain higher level.
It is more appropriate perhaps to think of this approach as constructing a "Game of Morphogenesis", but a game in which the motivation is to approach as closely as possible to the strategies employed by actual living organisms (Cf. [Cummings, 1994]). The extremely complicated cellular molecular machinery will be viewed as constructed to carry out the higher level mission. Even the cell itself will be viewed as macromolecular "robot" devoted to the collective task of the highly co-ordinated morphogenetic movements.
Side by side with "classic" theoretical biology approach there is a growing branch of Artificial Life approach to modelling of mechanisms of development [Mjolsness et al., 1991; deBoer et al., 1992; Kitano, 1994]. There are already works aimed at including simple morphogenetic models in evolutionary simulations [Mjolsness et all., 1991; Cangelosi et al., 1994; Dellaert and Beer, 1994a;b]. The main idea of this approach is to encode rules that will themselves self-organise to produce a phenotype, as is the case with biological morphogenesis. It is believed that intrinsic properties of these developmental processes, when used in conjunction with Genetic Algorithms, will lead to much more complex morphologies than those achievable with direct mapping [Dellaert and Beer, 1994a; Rocha, 1995].
In the past there has been very much effort devoted to questions of "pattern formation" and "morphogenesis". In many cases the geometry of a (usually flat) surface has been prescribed, and a "Turing-like" non-linear system of reacting and diffusing biochemicals have been investigating (For citations See [Harrison, 1987]). Most applications of reaction-diffusion approach to morphogenesis have assumed a pattern-forming region of fixed size and shape with fixed boundary conditions. Hence, the change of shape and form (the morphogenesis of its own!) which is thought to be a consequence of these primary patterns, was not considered. However other approaches have considered the geometric changes due to morphogenetic movements of epithelial surfaces [Gierer, 1977; Odell et al., 1981; Mittenthal and Mazo, 1983; Belintsev et al., 1987; Beloussov, 1991].
Morphogenesis, as distinct self-organising processes, requires effective non-linear feedback between its dynamic components [Beloussov et al., 1994]. This feedback should, on one hand, rapidly and precisely trace the deformation of embryonic layers caused by active mechano-chemical processes and, on the other hand, affect these very processes. It is the approach of coupling a morphogen to geometrical changes, and having the geometrical changes in turn give rise to a change in the morphogen pattern, and so on, which is employed here, as an extension of the same approach of previous works [Spirov, 1992; 1993a,b; Cummings, 1990; 1994].
Recently I considered a system of Turing-like equations coupled to geometric changes, which in turn couple back to alter Turing diffusion coefficients. In other words, I use known idea of coupling of one pattern to the formation of another. Using this approach I analysed the breaking of symmetry in early development of sea urchin. I briefly review the main results of previous works and consider new results in axis tilting as the case of symmetry breaking via secondary bifurcations. Particularly, a very simple algorithm of making of secondary bifurcations results in transition from initial unipolar gradient pattern to bipolar pattern with axis tilting.
I hope that my results will contribute to understanding of mechanisms of morphogenesis, both in its own rights and as an approach to artificial morphogenesis, such as development of Dellaert & Beer's autonomous agents [Dellaert and Beer, 1994a;b].
2. Pattern-Form Interplay and Symmetry Breaking in Early Development
The formation of the gastrula results from the activity of a simple epithelium (blastula wall, one cell thick). Gastrulation is itself a process whereby the basic plan of the organism is established as a tube within tube, endomesoderm within an envelope of ectoderm. There is an initial flattening, and often a thickening, of the vegetal region of the blastula to form the vegetal plate, and then pushing of this plate as an invagination. The early embryos of many species undergo form changes almost entirely by expansion and folding of a simple epithelium, much as sketched above (Fig.1).
A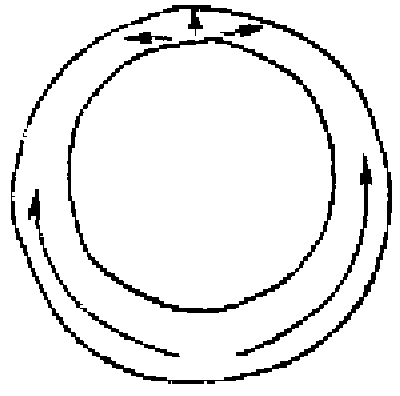 B
B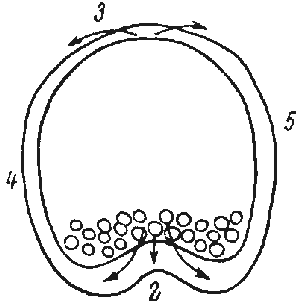
C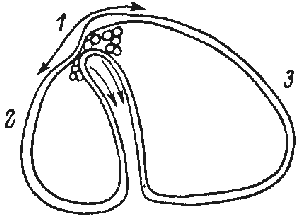 D
D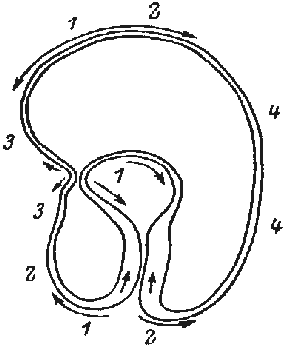
FIG.1. Symmetry and topological rearrangements in a course of echinids embryo development Stages of early embryogenesis of echinids show development as interplay of physiological gradients (indicated by arrows) and following morphogenetic movements (Sketched according to Child [1936]). Ciphers indicate relative levels of the gradients.
A-B. Stages of early gastrula;
C-D. Late gastrula.
Let us overview schematically the changes in symmetry considering as an example the morphogenesis of sea urchin embryo from the blastula stage (Fig.1). By the symmetry criteria this period of development could be subdivided into the following stages (Belousov, 1987)
In this article we will pay attention on the mechanisms of decreasing of symmetry order (desymmetrization) from m*µ symmetry to 1*µ one.
The events resulting in specification of cell lineage are a necessary prelude to actual morphogenesis that forms a sea urchin embryo [Wilt, 1987]. The activities of the individual cells and their responses to cues that transcend domains of single cells drive the formation of the embryo. These morphogenetic activities in turn undergo further refinements in the definition of the pattern of differentiation. It is appropriate to inquire how the determination in early stages causes morphogenetic movements and how these movements in turn lead to further pattern specification and differentiation.
The case at hand is a very complex, highly correlated cellular machinery [Cummings, 1994]. Epithelial sheets can remain as connected entities while folding, invaginating, and deforming to produce a variety of three-dimensional structures. The linkage of cells into epithelia provides a means of converting mechano-chemical cell activity into particular kinds of larger scale mechanical motion and reordering, with important consequences for form.
The different molecular events must apparently be interconnected but how this happens in detail is not known. What seems to be required is a place-dependent dynamic regulatory loop that ranges from the gene, through the gene products, to the cell layers, and back from the structures of higher order to control the expression of the same gene or a different gene [Edelman, 1988].
3. Game of Morphogenesis
Although a large literature exists for equations which specify fields of values in the plane with specified boundary values, or sphere, little or no literature exists for the case where the "morphogen field" interacts with the surface to change its shape, and the field in turn is itself changed because of the surface changes, and so on (see also [Cummings, 1985; 1989; 1990; 1994; Spirov and Boinovich, 1985; Spirov, 1992; 1993a,b]). While considering shape changes it is important to take into account both mechanical forces and the chemical-kinetics, and their both equally deserving of inclusion in the differential equations. However, in the pattern-form interplay model we explore the possibility that the secondary role of mechanics can be represented algorithmically [Cummings, 1985; 1989; 1990; 1994; Spirov, 1992; 1993a,b; Harrison and Kolar, 1988]. Certainly, the present model of morphogenesis is capable at best provide only an insight into such a complex process, and only on the highest scale, that is on the level of the cell ensembles.
3.1 Equations for morphogens
All Turing-like models require two diffusing substances as a minimum, [X] comparatively slow-diffusing one and [Y] that diffuse much faster [Lacalli & Harrison, 1991]. All 2-morphogen models require X-autocatalysis and cross-inhibition via a second species, Y. Y can be inhibited or depleted by X formation but activates the latter, as in the Brusselator. Symmetric 4-morphogen systems (with paired Xs and Ys, as in the case of dual Brusselator) belong to models with the general attributes of mutually exclusive states for production of each of two self-activating morphogens that are cross-activated via two further, faster diffusing morphogens.
We use here, following other authors [Harrison, Kolar, 1988; Harrison et al., 1988], the Brusselator as a system that has been extensively studied in relation to chemical pattern formation, as well as dual Brusselator as system with perfect interpretation in molecular biology terms [Lacalli, 1990]. Namely, assuming that the morphogens involved in gradient formation are primary gene products and not metabolites, the main steps in the reaction scheme leading to X and Y formation must represent some combination of gene transcription processes. This implies considerable complexity of regulatory control. The model specifically requires the presence of multiple inputs, including the gene self-activation by products [Lacalli, 1990].
We consider the application of these ideas to the object-oriented modelling of specific morphogenetic processes such as gastrulation of sea urchins. Initially the model describes geometry of a spherical layer. The program considers each of about 1000 cells as CELL-object with known space co-ordinates of 6+6 apexes and local concentrations of Xs and Ys. LIST of all CELL-objects is used for generation of new object "GASTRULA". Then procedure MOVE.TO changes local cell co-ordinates of the GASTRULA according to local Xs concentrations. Each cell produces and exchanges the morphogens X(s) and Y(s) in conformity with Brusselator or dual Brusselator model. The set of parabolic equations is solved by the finite difference method.
A predominant animal-vegetal polarity axis of the zygote is reflected in the model by appropriate boundary conditions: fixed concentration of the morphogen(s) X(s) on the vegetal pole and zero concentration on the animal pole. Under certain initial conductivity of cell-to-cell communications the trivial homogeneous distribution of morphogens is unstable.
Steps in computation of the morphogen distribution must alternated with steps in which the new morphogen distribution is used to govern morphogenetic movements. At odd numbered steps, numerical integration of the equations was carried out until a steady state was reached. At even numbered steps, "translation" of new patterns into new forms occurs by means of "morphogenetic movements". The reaction-diffusion pattern continually reorganizes itself in response to the shape change of the simulated object and this change occurs because of the existence of the pattern (Cf. [Harrison and Kolar, 1988]).
3.2. Morphogenetic movement algorithms
Morphogenetic movements of invagination begins in sea urchin embryo via apex constriction of initial cells at the blastula vegetal pole [Amemiya, 1989]. As a result, neighbouring cells were initially pulled toward the first cells by their contraction. The neighbouring cells appeared to respond to the stretch by their own apex constriction. This pulled the next group of adjacent cells. This wave of apical constriction was thus spread from the vegetal pole and radiates outwards.
According to the model morphogen-induced morphogenetic movements are somewhat separated in time. It should be stressed that the morphogen pattern develops first, followed by the appropriate morphogenetic movement (geometric change). This feedback loop from the morphogen patterns to changes in surface geometry is determined by cell form changes (namely columnarization of cells and/or cell apex constriction) which are dependent on X-concentration. The particular examples of elementary cell shape transformations are shown in Fig.2.
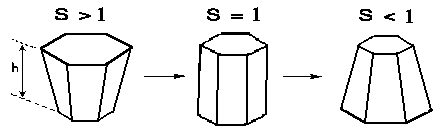
FIG.2. The variation of shape of cells with morphogen concentration for the case of symmetric distortion. "S" is the ratio of local basal to apical cell surface area, and "h" is the local sheet thickness. The height "h" is assumed to stay constant in this figure. (According to [Cummings, 1994].
Fred Cummings [1989; 1990; 1994] has been studied elementary expressions for the gauss curvature K in terms of the parameters s, the ratio of local basal to apical cell surface area, and h, the local sheet thickness. The sheet thickness and the basal to apical ratios were presumed to be a slowly changing function of cell position.
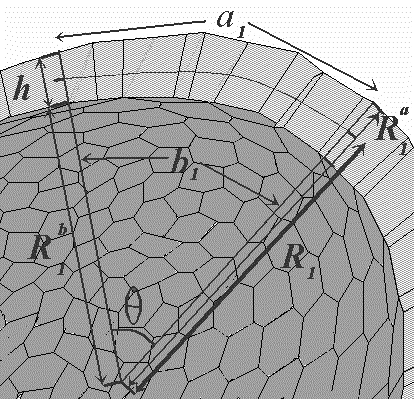
FIG.3. A cross-section through the cellular monolayer along one principal direction in the surface. See text for details.
Figure 3 presents a section of the sheet, which indicates a gradual change in both h and s, as we read from left to the right of the picture. The apical area is indicated as "a" in the figure, and the basal area as "b". Also shown are the three radii Ra,1, Rb,1, and R1; Ra,1 and Rb,1 are the radii of curvature of the apical and basal areas respectively, in the "number one" direction, and R1 is the corresponding radius of curvature of the middle surface, which is shown as a dashed line. The corresponding quantities in the orthogonal direction (into the page), that is, the Ra,2, Rb,2, and R2 are not shown.
The problem at hand is to relate the radii of curvature to s and h, and thus to K, which is related to R1 and R2 by K = 1/ (R1*R2).
Elementary solution of this task, according to Cummings, gives
 (1)
(1)
Thus, empirical knowledge of the dependence of s and h on the morphogen m will determine the gauss curvature at each point on the surface. It seems reasonable to presume, for example [Cummings, 1994], that both of these functions s(m) and h(m) are monotone functions of m, perhaps even the "S"-shaped functions, which often are used for description of biological processes. In the MOVE.TO procedure we assume that s(m) and h(m) are "S"-shaped functions of m.
4. Pattern-Form Interplay in the Model
It seems that morphogenesis is based on interactions between the genome inside each cell nucleus and the "environment" of neighbourhood cells of the multicellular layer. Cells are thought can test its local (bio)mechanical environment by sensing local changes in the layer geometry. Once the cell’s cyto-mechanical sensors receive the signal about completion of appropriate morphogenetic movement, they transduce this "message" into the nucleus. The individual nucleus responds by triggering the appropriate gene cascade for the cells located at the definite position of multicellular layer. The initial signal is purely mechanical but the response is biochemically sensed, enhanced, and mediated by commonplace cell regulatory mechanisms [Bjorklund and Gordon, 1993]. In this way the organism acquires the required cells, in the right place, and at the right time.
One of the ways for effective feedback from pattern to form is assumed to be the exploitation of the cell feature to sense the curvature of the substratum [Fisher & Tickle, 1981]. According to Dunn and Heath [1976], fibroblasts movements across the substratum are inhibited if the curvature does not allow the cytoskeletal elements to retain linear integrity, because microfilament bundles cannot operate if bent.
A simplest and effective mechanism of local cell respond to completion of appropriate morphogenetic movement consists in differentiation of intercellular contacts. In this case the feedback loop from the surface geometry to morphogen pattern is determined by the change in cell- to-cell conductivity (proportionally to local curvature in that part of the cell layer, wherein the morphogenetic movements have occurred). This is in a close agreement with known data on development of the cell-to-cell communication system at sea urchin gastrula [Caveney, 1985].
The above discussed rules of pattern and form interactions are described by following general set of equations:
 (2)
(2)
Xi and Yi are concentrations of intermediates of the Brusselator in the i-cell; a and b are parameters; DXi and DYi are position-dependent diffusion coefficients; Ki is local gauss curvature (in vicinity of the i-cell); e is parameter; S(Xi) is "S"-shaped function of Xi.
In my previous work [Spirov, 1993] I used such simple algorithm for 3D graphic realisation of local gauss curvature dependence on local morphogen concentration. Translation of the X gradient in the areas where X > Xcr. was carried out by means of morphogenetic movement in accordance with formula:
![]() (3)
(3)
where R(tn) is the radius-vector of the inner surface of the model at the stage tn (present stage), R(tn-1) is the radius-vector of the surface at a previous stage, q is empirical parameter.
In the same paper I used following expression for diffusion coefficients Dj as function of the local gauss curvature or the local increment of the radius-vector R of the surface which, in turn, is a function of X:
![]() (4)
(4)
DJt1 is a local diffusion coefficient at the recent stage t1, DJt2 is a local diffusion coefficient at the previous stage t0, p is empirical coefficient.
In case of more refined modelling, depicted in Fig.5 the program was tested with more precision iterative procedures for approximation of radius-vector (gauss curvature) dependence on X, but qualitative behaviour of the model is turned to be insensitive to peculiarities of algorithms.
4.1. The change of initial symmetry in morphogenesis simulation
Carrying out a number of computer experiments with the model reveal that it behaviour is similar to early stages of sea urchin morphogenesis. The model simulates flattening of a blastula bottom, invagination, elongation and subsequent morphological metamerization ("chambering") of a "gut" with maintenance of an initial axial symmetry (an animal-vegetal axis), as well as determination and invagination of an "orus" (i.e. determination of a second axis of symmetry: an oral-aboral axis).
Several modes of the model behaviour are possible:
All three developmental pathways are described in [Spirov, 1993]. In case (1) there occurs a secondary bifurcation from a simple gradient, described by spherical harmonics Y11, to the pattern, described by spherical harmonics Ylm with a non-zero value of order m (Fig.4).
a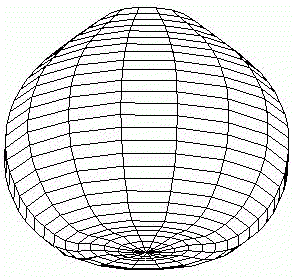 b
b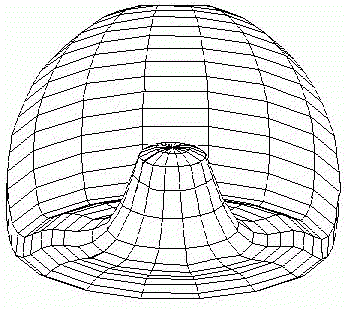 c
c
FIG.4. First scenario of the pattern-form interplay in the model of sea urchin early development with change of initial axial symmetry into bilateral [Spirov, 1993a].
Values of parameters of the Brusselator are a =3; b =15; initial values of transport coefficients are D0X=110; D0Y=30; boundary conditions are XNorth pole=7.0; XSouth pole=0.0; dYNorth pole/dt=0.0; dYSouth pole/dt=0.0.
A front wall of the model figures are removed in all pictures.
In case (2) the time series of the morphogen patterns are formally described by spherical harmonics of general form Yl0 with zero order parameter, i.e. the processes in the model maintain axial symmetry.
In the case (3) determination of the second axis of symmetry and the invagination not only of a "gut", but also of an "orus" was established (Fig.5). Thus we achieve such biologically essential case of symmetry breaking (from m*µ symmetry to 1*µ one) via axis tilting. This symmetry breaking by tilting of initial axis of symmetry as a consequence of secondary bifurcation is the main subject of interest in remaining part of the paper.
A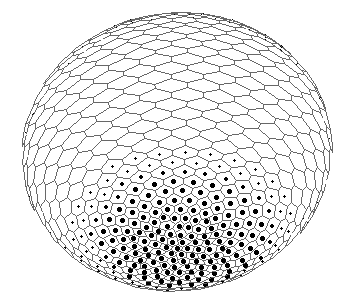 B
B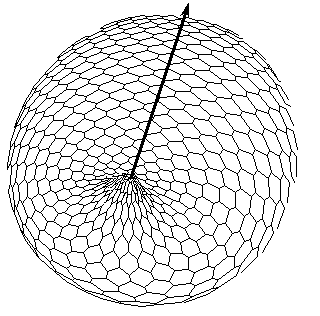 C
C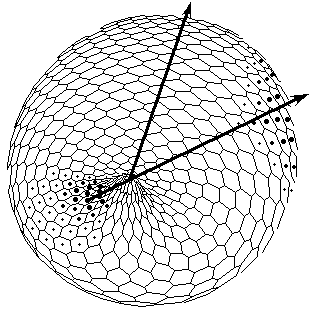 D
D
FIG.5. The axis tilting phenomenon in the Pattern-Form Interplay Model.
A. An initial state of the model with spontaneously generated concentration gradient (for Brusselator RD system) with maximum at the "North" pole and minimum at the "South" pole of the spherical multicellular layer. The more blue are 'nuclei' inside a cell, the more are local concentrations of one of the Brusselator intermediates [X].
B. Simulation of invagination and formation of gastrula. Form of the model after "translation" of the X-gradient on Fig.A according to iteration algorithm for solving the Eq.(1).
C. Bipolar pattern as steady state established in Brusselator RD system with position-dependent diffusion coefficients. The one pattern is coupled (Fig.A) to the formation of the other. New pattern differs not only in overall geometry but also in tilting of the axis as compared with initial gradient.
D. Form of the model after translation of the secondary bipolar gradient on the Fig.C. We achieved both the continuation of the morphogenetic movements of invagination and the initiation of invagination of "orus".
The dynamics of (bio)chemical pattern observed in our computer experiments and its relation to the morphogenetic movements are in close agreement with classical results obtained by Child [1936] in his works on physiological gradients in echinoderms development (Cf. Our Fig.4 with Fig.1), as well as with modern data on region-specific gene expression prior and at gastrulation in sea urchin embryo [Wilt, 1987; Davidson, 1989; Livingston, Wilt, 1990].
5. Discussion
Bifurcation in nonlinear PDEs is a well-known mechanism for spontaneous pattern formation. Autocatalitic reaction-diffusion systems have been shown to undergo such bifurcations, and stable inhomogeneous concentration patterns arise (Turing structures). Such systems have been studied extensively both analytically and numerically as they may play an important role in spontaneous biological pattern formation.
According to Harrison [1981], morphogenesis is the creation of a complicated shape out of a simpler one by chemical processes in living organisms. The essence of it is symmetry-breaking.
The tilting of initial gradient to secondary “oral” axis which we found for closed layers reminds recent results of [Hunding, 1987; Hunding and Brons, 1990]. Axel Hunding [1987] numerically and analytically investigated secondary bifurcation points for three-dimensional spherical reaction-diffusion system, when initial symmetry is broken by making diffusion- and rate-coefficients functions of primary gradient.
It is well-established that one of the concentration patterns which has been shown to arise in RD-systems in a spherical region, is a gradient pattern, with high concentration at one spontaneously generated pole, and low concentration at the opposite pole of the sphere. It has been argued by many authors, that such a pattern might be the pattern governing the formation of animal-vegetal (“North” and “South”) poles in the developing egg. It was assumed, that this steady concentration gradient affects the parameters in a second, otherwise independent, Turing-like system (namely, Selkov model) [Hunding, 1987] Thus, Turing structures of the first kind are given by the standard equations
![]() (5)
(5)
whereas Turing structures of the second kind arise from equations with position-dependent parameters (diffusion-constants, in this case)
![]() (6)
(6)
where r is radius-vector, Cj is concentration of j-intermediate, Dj is its diffusion-constant, Fi,j.(Ci) are a kinetic parts of a model.
It was shown, that such a very simple modification of the basic Turing-type RD equations results in bipolar patterns having orthogonal orientation with respect to initial polarity of the system. Hunding’s result that the emergence of the perpendicularly oriented bipolar pattern obtains in a broad class of chemical reaction systems is an important general result for understanding of early morphogenesis. They explain the emergence of a bipolar order orthogonal to the animal-vegetal axis in the cleaving egg.
As is the case of Hunding’s [1987] numerical simulations in three dimensions, my numerical simulations in two dimensions of a closed axis-symmetrical surface show the axis tilting phenomenon. Thus the axis tilting bifurcation may be introduced by coupling of the initial gradient to the second Turing-like system both in a sphere (cleaving egg model) and in a closed surface (gastrula model). However, in my calculations, a new axis was not orthogonal to initial one (Fig.5). Secondary axis establishment is one of the mysteries of developmental biology and I hope that my computational results could help to reveal it.
Acknowledgments
Supported by Russian Foundation for Basic Researches (Grants No 96-04-49349 and No 96-04-49350). The author wishes to thank Fred Cummings and Axel Hunding for stimulating discussions on general aspects of morphogenesis, Lionel Harrison, Truston Lacalli and Lev Beloussov for reprints of articles and Maria Samsonova for critical reading of the MS.
References