Where Sun always shine...

PROJECTS

   Josephson Junction Simulation

Introduction
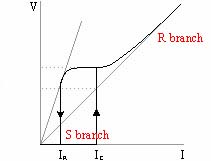As said elsewhere a Josephson junctions is formed "weekly" connecting two superconductive electrodes. The current-voltage curve of a typical real Josephson junction is illustrated in the figure on the left. We can distinguish two separate branches: the S (Superconductive or Stationary) branch and the R (Resistive) branch. It turns out that this behavior is "quite" equivalent to the parallel of a capacitor, a not linear resistance and a quantum phase driven current source. This model goes under the acronym RCSJN (Resistively Capacitively Shunted Junction Not linear), an extension of the original Stewart-McCumber model in which was considered only a vanilla (i.e. linear) resistance.
Given that the quantum phase driven current is governed by Josephson phase-voltage relations which are already not linear, Kirchoff rules for the parallel produce a second degree not linear equation in the quantum phase. A numerical integration method is used to resolve the system and to evaluate phase-space trajectory. From the trajectory you can estrapolate various information including the current-voltage curve and the asyntotic behavior (i.e. the attractor).
Numerical integration methods used
A numerical integration method is the core of every program belonging to this project. Some program can use an user selected method while some stick with an hardcoded one. Following is a list of the methods currently implemented: Adaptive Runge-Kutta and Bulirsch-Stoer methods were evaluated but not used.
The table below shows the ITest benchmark results for the implemented methods on my machine.
 
 
 
Time in seconds to integrate RCSJN model over 10 millions steps
Adams III 20
Adams IV 21
Adams-Moulton V 37
Adams-Moulton VI 38
Runge-Kutta IV 77
The programs
ANSI C applications     Downloadable Win32 applications (compiled for Pentium+ machines) and ANSI C sources are here.
Please note that no manual/document/explanation is included (sorry but I do not have enough time for that); however you can request info at my address.

 silly Java 1.1 application

    Downloadable Java 1.1 sources and classes (compiled with Sun's JDK 1.1.4) are here.
Please note that no manual/document/explanation is included (sorry but I do not have enough time for that); however you can request info at my address.

 in the works

    Shepp-Logan 3D Phantom synthetizer

    Introduction
The Shepp-Logan 3D Phantom (SL3DP) is a standard 3D phantom used to simulate medical image reconstruction algorithms. The SL3DP is defined by the superimposition of 12 ellipsoids each having a slightly different density. While the SL3DP was mainly thought for human head simulations, it is believed to represent rather well the generic radiological problem to discriminate small density discontinuities which can suggest a tissue lesion. Each ellipsoid belonging to the phantom is defined as in the figure on the left. Below you can find the table listing each ellipsoid definition.
 
 
Shepp-Logan 3D definition by superimposition of 12 ellipsoids
Center coord x Center coord y Center coord z 1st semiaxis a 2nd semiaxis b 3rd semiaxis c Equatorial angle Polar angle Density
0.0 0.0 0.0 0.69 0.9 0.92 0 0 2.0
0.0 0.0 -0.0184 0.6624 0.88 0.874 0 0 -0.98
-0.22 0.25 0.0 0.41 0.21 0.16 0 72° -0.02
0.22 0.25 0.0 0.31 0.22 0.11 0 -72° 0.01
0.0 0.25 0.35 0.21 0.35 0.25 0 0 0.01
0.0 0.25 0.1 0.046 0.046 0.046 0 0 0.01
-0.08 0.25 -0.605 0.046 0.02 0.023 0 0 0.01
0.06 0.25 -0.605 0.046 0.02 0.023 0 90° 0.01
0.06 -0.625 -0.105 0.056 0.1 0.04 0 90° 0.02
0.0 -0.625 0.1 0.056 0.1 0.056 0 0 -0.02
0.0 0.25 -0.1 0.046 0.046 0.046 0 0 0.01
0.0 0.25 -0.605 0.023 0.023 0.023 0 0 0.01
    The program
The synthetizer program syntax is: where xcube, ycube, zcube are the dimensions (in pixels) along x, y and z axis. A binary data file (sl_pha.dat) is saved containing full floating values per voxel. The optional X, Y and Z switches tell the program to save also section images using portable grey map (PGM) binary format.
Currently the synthesis is done on the cube of real dimensions 2x2x2.

    Request ANSI C++ sources and/or Win32 apps

    Shepp-Logan 3D Phantom projector

     Introduction
In order to simulate cone beam 3D CT you need to simulate 2D projections. In this case the projector provide to project the Shepp-Logan 3D Phantom (SL3DP). Given SL3DP projections you can test your backprojector by comparing recostruction values (i.e. density spatial distribution) with "true" values obtained using slps.
    The program
The projector program syntax is: where detsw and detsh are the plane detector semiwidth and semiheight and where numpro are the number of projections (that is the projection angle moves from 0 to 2PI in 2PI/numpro quanta). Please note that currently the plane detector and X source position are hardcoded and that the detector is not curved (i.e. semicylindrical surface) but strictly plane.

    Request ANSI C++ sources and/or Win32 apps

    Cone beam 3D filtered backprojector

     Introduction
The cone beam 3D filtered backprojector should reconstruct a solid 3D object by opportune elaboration of its 2D cone projections. An approximate reconstruction algorithm was provided by Feldkamp, Davis and Kress (hence the name of FDK algorithm) in the eighties. The algorithm is quite simple but somewhat computationally intensive.
    The program
The cone beam program syntax is: Currently the reconstruction is done on a 128x128x128 3D cube (hardcoded) using bilinear interpolation. Results are quite good (see below).

    Request ANSI C++ sources and/or Win32 apps

    About performance
The FDK algorithm is tricky to optimize any further. The version currently available is written using floating-point-math. Below you can see the performance results on my machine for the reconstruction on the given volume for 40 256x256 projections (bilinear interpolation).
 
FDK Cone Beam reconstruction performance
Reconstruction step
64x64x64 cube (2 MB)
128x128x128 cube (16 MB)
256x128x256 (64 MB)
FFT + Filtering + FFT -1 11 sec 11 sec 11 sec
FDK Backprojection 13 sec (half a min total) 110 sec (2 min total) 570 sec (9 min total)

Note the memory occupation for the given array of doubles. Consider that even at 256x128x256 MB Win NT is bogged down by virtual memory. That was the reason why I did not test on a 256x256x256 cube. The memory occupation would reduce by a factor 2 using floats instead of doubles. Btw you really need 128 MB (physical) and fast virtual memory (i.e. HDs) to take the reconstruction on more detailed volumes.

I've thought many times about ways of making the algorithm any faster. The thing I've noted is that the most time-consuming operation is pixel interpolation. In particular float-to-integer conversions seems to be the main reason of slowness. These conversions are mandatory even in order 0 (nearest neighbour) interpolation: bilinear interpolation introduces another bog-down factor but that is not crucial in my opinion.
These facts can suggest to ditch floating-point-math and use fixed-point-math: in fixed-point-math (fpm) the conversion to integer is pretty istantaneous (just a bit shift). fpm was the main way of representing real numbers in the good old days of computing when fpu processors were very expensive. In those days cpus did not include floating-point units (do you remember 68030/68882 ?) and so programmers had to program using fpm. Nowadays every cpu includes a fpu so many programmers recommend not to use fpm just because it's not any more convenient. Hey even Quake does not include fpm anymore! Consider moreover that using the fpu is a kind of free-lunch cause the fpu can work in parallel with the cpu integer unit: the amount of parallelism is clearly application dependant, for the cone beam reconstruction however I expect the parallelism to be quite low.
fpm has its flaws (lack of general precision) but these are not important in a not so demanding application as a cone beam reconstruction program. The main problem with fpm nowadays is lack of support: no standard math library, you have to code basic (and not so basic) operations in assembler. I think this kind of work is not feasible for me right now. If anything changes about this project (more interest) I may reconsider though.

    Sample images
Below you can find the comparison between the most interesting sections of the "exact" Shepp-Logan phantom and the reconstructed ones (via cbct). Every section was calculated on a 128x128x128 voxels 3D cube starting from 64 projections on a detector plane of 128x128 pixels. As you can see results are quite good even using few projections and low resolution geometry.
 
Exact section Reconstructed section
Plane xz.
79 y section (y = + 0.234).
Plane xy.
40 z section (z = - 0.375).
Plane xy.
90 z section (z = + 0.406).

    1D Fourier Farm wrapper

     Introduction
Around the Internet you can find many Fast Fourier (1D) implementations. During a research job of mine I have tested the majority of public domain FFT libraries for Windows 9x/NT/2000. My conclusions were:
  1. If you need to transform 2^n points, use Intel Math Kernel Library. Look at  http://developer.intel.com/vtune/perflibst/mkl/index.htm.
  2. If you need more general transformations, use the Fast Fourier in The West. Look at http://theory.lcs.mit.edu/~fftw/.
Intel MKL (version 3.1 at the time of writing) is provided as Windows DLLs and is rather huge (> 1 MB).
FFTW (version 2.1 at the time of writing) is provided as GNU C source code.
    The wrapper
My FourierFarm wrapper is a 1D Fourier Transform Win32 DLL. The only exported function provided by FourierFarm.dll is

   < FourierFarm* GetFourierFarm_Best(int npToPad,bool isPad) >

where npToPad is the number of points requested for transformation, isPad a flag for zero padding and FourierFarm* a pointer to a C++ class with which apply FFTs to 1D arrays.

The actual FFT code used depends on the presence of FFT libraries. If Intel MKL library is found and the number of points is of kind 2^n, then MKL code is used. If the number of points is not a power of 2, the wrapper looks for FFT libraries in this order: FFTW, MKL. If nor MKL nor FFTW libraries are found, the wrapper uses the built-in FFT code based on Duhamel split-radix algorithm written by me in the past.

    Requirements

The wrapper is useful for C++ developers only.
If you intend to use Intel MKL code, look at the Intel Developer site http://developer.intel.com/vtune/perflibst/mkl/index.htm and install MKL libraries (*.dll) in the system/system32 directory.
If you intend to use FFTW code, download from http://theory.lcs.mit.edu/~fftw/ the FFTW source code. Then you will need to build a fftw.dll library from fftw/rfftw sources. Move the fftw.dll so created in the system/system32 directory.

    Download Win32 FourierFarm.dll and C++ header

    Request Win32 C++ sources

Stefano Agostinelli - agostinellis@bigfoot.com
 
 


This page hosted by  Get your own Free Home Page





1