Vladimir Zabrodsky: Three Selection Algorithms



	FIND SELECT MODIFIND

A comparative study of three selection algorithms, and their implementations in the Rexx language, for finding Kth smallest of N elements: Hoare's FIND, my modification of FIND (MODIFIND) and Floyd's and Rivest's SELECT.

The selection problem can be stated as follows (C. A. R. Hoare in [1]): given an array A of N distinct elements and an integer K, 1 <= K <= N, determine the Kth smallest element of A and rearrange the array in such a way that this element is placed in A[K] and all elements with subscripts lower than K have fewer values and all elements with subscripts greater than K have greater values. Thus on completion of the program, the following relationship will hold:

A[1], A[2], ..., A[K- 1] <= A[K] <= A[K+ 1], ..., A[N]

The usefulness of a solution of this problem arises from its application to the problem of finding the median or other quantiles or finding the minimum or the maximum or second-largest elements ... Straightforward solution would be to sort the whole array. But if the array is large, the time taken to sort it will also be large. I'll introduce a faster algorithm due to C. A. R. Hoare. He called his program FIND (I'll refer to the implementation in this article as H) and it selects the Kth smallest element in just O(N) average time.

The H algorithm

Hoare's algorithm is based on the following corollary of the obvious definition:

DEFINITION

Kth smallest element of N elements is a unique element which is greater than K - 1 other elements but less than N - K elements.

COROLLARY

An element can't be Kth smallest when it is greater than K (and more) elements or less than N - K + 1 (and more) elements.

We begin with a conjecture: A[K] is Kth smallest. The algorithm of the proof or rejection this conjecture is: The array is divided by scanning from the left (for indexes I = 1, 2, ...) to find an element A[I] >= A[K], scanning from the right (for indexes J = N, N - 1, ... ) to find an element A[J] <= A[K], exchanging them, and continuing the process until the pointers I and J cross. This procedure gives three cases:

CASE 1 (J < K < I)

Q. E. D. Kth smallest element is in its final place and the program finished. Example:

CASE 2 (J < I <= K)

A[1] ... A[J] are less than N - K + 1 other elements, exactly they are less than N - I + 1 >= N - K + 1 elements. I. e. any one can't be Kth smallest, so we'll find (K - I + 1)th smallest element in the subarray A[I] ... A[N]. Example:

CASE 3 (K <= J < I)

A[I] ... A[N] are greater than K other elements, exactly they are greater than J >= K elements. I. e. any one can't be Kth smallest, so we'll find Kth smallest element in the subarray A[1] ... A[J]. Example:

The following program H ilustrates this algorithm. It is the translation Niklaus Wirth's program from [6] to the Rexx language.

H: procedure expose A. parse arg N, K L = 1; R = N do while L < R X = A.K; I = L; J = R do until I > J do while A.I < X; I = I + 1; end do while X < A.J; J = J - 1; end if I <= J then do W = A.I; A.I = A.J; A.J = W I = I + 1; J = J - 1 end end if J < K then L = I if K < I then R = J end return

The analysis of the H algorithm

Let us determine the number of comparisons, as A.I < X is, and swaps W = A.I; A.I = A.J; A.J = W that H makes. Let C(N, K) be the number of comparisons made by H when applied to finding Kth smallest of N elements, and let S(N, K) be the number of swaps of items.

In worst case:

C_max(N, 1) = C_max(N, N) = (N² + 5N - 8) / 2
C_max(N, K) = (N² + 5N - 12) / 2, for K = 2, 3, ..., N - 1

In [3] I showed examples of arrays for worst cases (Kth position is red coloured):

for K = 1:    N    2    1    3    ...    N-1
for K = 2:    1   N     2    3    ...    N-1
for K = 3:    3    2    N    1    4    5    ...    N-1
for 3 < K < N-1:    2    ...     K-2    K    K-1    N    1    K+1    ...    N-1
for K = N-1:    2    ...    N-1    1    N
for K = N:    2    ...    N-2    N    N-1    1

In average case (D. E. Knuth in [2]):

C(N, K) = 2((N + 1)H_N - (N - K + 3)H_{N - K + 1} - (K + 2)H_K + N + 3)

where

H_N = 1 + 1/2 + ... + 1/N

This yields as special cases:

C(N, 1) = C(N,N) = 2N + o(N)
C(N, median)= 2N(1 + ln2) + o(N) = 3.39N + o(N)

I proved:

S(N, K) = (1 / 3)((N + 1)H_N - (N - K + 2.5)H_{N - K + 1}- (K + 1.5)H_K + N + 2)

Corollary:

S(N, 1) = S(N, N) =H_N
S(N, median) = (1 / 3) ((ln2 + 1)N - 3lnN) = 0.56N + o(N)

The Z algorithm

We consider the array 1, 10, 2, 3, 4, 5, 6, 7, 8, 9, and K= 2. The array is split into two parts A[1], ..., A[9] and A[10]: 1, 9, 2, 3, 4, 5, 6, 7, 8 and 10 by the help of one swap and 12 comparisons. But when I find that 10 is greater than two elements (1 and 9) then I know: it can't be second smallest element. I can reach the same result (1, 9, 2, 3, 4, 5, 6, 7, 8, 10) by the help of one swap and three comparisons and I'll search second smallest element in the subarray A[1], ..., A[9]. This modification of the H algorithm describes the program Z. It is the translation to the Rexx language from my article [3], I called it MODIFIND for Algorithms, Data Structures, and Problems Terms and Definitions of the CRC Dictionary of Computer Science, Engineering and Technology:

Z: procedure expose A. parse arg N, K L = 1; R = N do while L < R X = A.K; I = L; J = R do until J < K | K < I do while A.I < X; I = I + 1; end do while X < A.J; J = J - 1; end W = A.I; A.I = A.J; A.J = W I = I + 1; J = J - 1 end if J < K then L = I if K < I then R = J end return

The analysis of the Z algorithm

In worst case

C_max(N, K) = NK + N + K - K² - 1, for K = 1, 2, ..., N

In worst case the number of comparison for the algorithm H doesn't depend on K. But for the algorithm Z the number of comparison depends on K. The following graph shows the time of execution H and Z in worst case.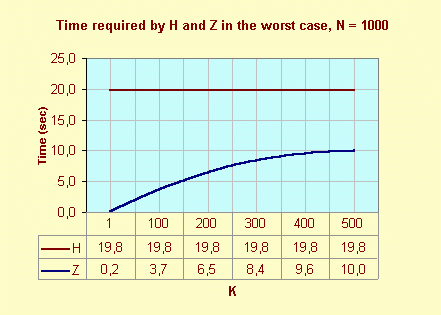

In average case

In [3] I state only values of C(N, 1), C(N, N) and S(N, K):

C(N, 1) = C(N, N) = N + H_N

S(N, K) = 0.5((N + 1) H_N - (N - K)H_{N - K + 1} - (K - 1)H_K)

This yields as special cases:

S(N, 1) = S(N, N) = lnN + o(N)
S(N, median) = 0.5(Nln2 + 2lnN) + o(N) = 0.35N + o(N)

The FR algorithm

In their article Expected Time Bounds for Selection[4] R. W. Floyd and R. Rivest presented a new selection algorithm SELECT which is shown to be very efficient on the average, both theoretically and practically. The number of comparisons used to select the Kth smallest of N numbers is N + min(K, N - K) + o(N). I express SELECT in the Rexx language as the FR program.

FR: procedure expose A. parse arg L, R, K do while R > L if R - L > 600 then do N = R - L + 1; I = K - L + 1; Z = LN(N) S = TRUNC(0.5 * EXP(2 * Z / 3)) SD = TRUNC(0.5 * SQRT(Z * S * (N - S)/N) * SIGN(I - N/2)) LL = MAX(L, K - TRUNC(I * S / N) + SD) RR = MIN(R, K + TRUNC((N - I) * S / N) + SD) call FR LL, RR, K end T = A.K; I = L; J = R W = A.L; A.L = A.K; A.K = W if A.R > T then do; W = A.R; A.R = A.L; A.L = W; end do while I < J W = A.I; A.I = A.J; A.J = W I = I + 1; J = J - 1 do while A.I < T; I = I + 1; end do while A.J > T; J = J - 1; end end if A.L = T then do; W = A.L; A.L = A.J; A.J = W; end else do; J = J + 1; W = A.J; A.J = A.R; A.R = W; end if J <= K then L = J + 1 if K <= J then R = J - 1 end return

Floyd and Rivest in [5] write: The arbitrary constants 600, 0.5, 0.5 appearing in the algorithm minimize execution time on the particular machine used.I experimentally found that constants 600, 0.5, 0.5 are the good choice. For classic Rexx there is a problem with functions LN, EXP and SQRT (they aren't built-in). But hundreds experiments for N = 10000 shown, that the maximum precisionnumeric digits 6 will be sufficient. Hence I used the following simple algorithms from textbooks:

EXP: procedure parse arg Tr; numeric digits 3; Sr = 1; X = Tr do R = 2 until Tr < 5E-3 Sr = Sr + Tr; Tr = Tr * X / R end return Sr

SQRT: procedure parse arg X; numeric digits 3 if X < 0 then return -1 if X=0 then return 0 Y = 1 do until ABS(Yp - Y) <= 5E-3 Yp = Y; Y = (X / Yp + Yp) / 2 end return Y

LN: procedure parse arg X; numeric digits 3 M = (X + 1) / (X - 1); Ln = 1 / M do J = 3 by 2 T = 1 / (J * M ** J) if T < 5E-3 then leave Ln = Ln + T end return 2 * Ln

I experimantally found that for achievement of the lowest average time is the best choice: the constant 3 in statement numeric digits and the constant 5E-3. For the lowest number of comparisons I found more candidates: sometimes 4 and 5E-3 or 5 and 5E-5 or 6 and 6E-6 ... I used 3 and 5E-3 because the FR program was fastest as well as. The results showed that the average number of comparisons for finding the median is proportional to 1.5N.

Comparisons of Algorithms

For comparisons I used the program as following one (this example is only for timing results and for K >= 500):

/* COMPARISON */ N = 10000 do K = 500 to 5000 by 500 TH = 0; TZ = 0; TFR = 0 do Trial = 1 to 100 call RANDARRAY; call INITIALIZE call TIME "R"; call H N, K; TH = TH + TIME("R") call INITIALIZE; call TIME "R"; call Z N, K TZ = TZ + TIME("R"); call INITIALIZE call time "R"; call FR 1, N, K TFR = TFR + TIME("R") end Trial say K TH/100 TZ/100 TFR/100 end K exit RANDARRAY: procedure expose B. N do J = 1 to N; B.J = RANDOM(1, 100000); end return INITIALIZE: procedure expose A. B. N do J = 1 to N; A.J = B.J; end return

As a measuring instrument I used my PC with 6x86MX-PR233 processor and 32MB RAM.

The graph Average time required H, Z, FR shows, that Z is faster than FR only for K = 1. I repeated a few times the measuring and always the finding of the median was faster than the finding of the K-th element, for K = 3000 or 4000.

The graph H, Z, FR - comparison count, average case explains previous results. It proves that the Knuth's estimate of the average case for the number of comparison for H holds, too. The Z algorithm is best only for K = 1 otherwise FR is the winner. The theoretical result for FR for the finding of the median holds, i. e. 1.5N comparisons.

The graph H, Z, FR - swap count, average case shows that Z has the least count of swaps. It shows that my estimate for S(N, K) for Z holds as well as.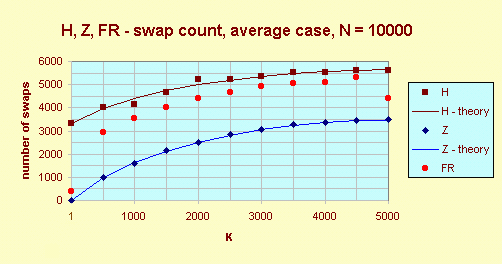

Conclusion

Algorithms Z and FR are always better than H; FR has fewer the number of comparison than Z; Z has fewer the number of swaps than FR.

For additional information see my page About MODIFIND.

Richard Harter's comment in comp.programming
It is interesting. One of the attractive things about the Z algorithm is that it is simple and easy to code. This is no small thing; quite often one is trading off coding time versus performance time. In any case it is nice to know where to find the algorithms on line.

Richard Harter, cri@tiac.net, The Concord Research Institute http://www.tiac.net/users/cri
What is the difference between Mechanical Engineers and Civil Engineers?
Mechanical Engineers build weapons, Civil Engineers build targets.

Literature
1. C. A. R. HOARE: Proof of a Program: FIND. CACM, Vol 14, No. 1, January 1971, pp. 39-45.
2. D. E. KNUTH: The Art of Computer Programming. Sorting and Searching. Addison-Wesley, Reading, Mass., 1973.
3. V. ZABRODSKY: Variace na klasicke tema.Elektronika (Czech magazine), No. 6, 1992, pp. 33-34.
4. R. W. FLOYD,R. L. RIVEST: Algorithm 489 The Algorithm SELECT - for Finding the ith Smallest of n Elements [M1].CACM, March 1975, Vol. 18, No. 3, p. 173.
5. R. W. FLOYD,R. L. RIVEST: Expected Time Bounds for Selection.CACM, March 1975, Vol. 18, No. 3, pp. 165-172.
6. N. WIRTH: Algorithms and data structures. New Jersey 07632, Prentice Hall, Inc., Engelwood Cliffs, 1986.