No vamos aquí a proporcionar una clase maestra sobre fractales, sino que vamos a mostrar que Java también se puede emplear para la implementación de algunos ejemplos clásicos de la geometría de fractales. Vamos a realizar por uno sencillito, en el que se trata de un conjunto definido por todos los números reales entre cero y uno, inclusive. Entonces, eliminamos el tercio central de ese conjunto, es decir, todo lo que se encuentre entre el primer tercio y el último, ambos exclusive.

Para visualizar lo anterior vamos a utilizar segmentos de línea. Eliminaremos el tercio medio del segmento, es decir, nos quedaremos con el segmento que va desde el inicio del segmento hasta el segundo noveno, y entre el séptimo noveno y el final; y continuaremos este proceso indefinidamente.

La verdad es que parece un poco confusa la explicación, pero si una imagen vale más que mil palabras, un buen programa Java vale más que mil imágenes. Por ello, aquí esta el código Java, Tercio.java, que muestra sucesivas líneas en que se demuestra la explicación del párrafo anterior.

import java.awt.*;
import java.applet.Applet;
import java.util.Vector;

public class Tercio extendsApplet {
    int apAncho,apAlto;
    Vector finPuntos = new Vector();

    public void init() {
        apAncho = size().width;
        apAlto = size().height;

        finPuntos.addElement( new Float( 0.0f ) );
        finPuntos.addElement( new Float( 1.0f ) );
        }

    public void paint( Graphics g ) {
        float x1,x2;
        Float tmpFloat;

        for( int i=0; i < apAncho; i+=5 ) 
            {
            // Pintamos las lineas
            for( int j=0; j < finPuntos.size(); j+=2 )
                {
                tmpFloat = (Float)finPuntos.elementAt( j );
                x1 = tmpFloat.floatValue();
                tmpFloat = (Float)finPuntos.elementAt( j+1 );
                x2 = tmpFloat.floatValue();
                g.drawLine( Math.round( x1*apAncho ),i,
                    Math.round( x2*apAncho),i );
                }
            // Eliminamos el tercio medio de las lineas
            BorraSegmentos();
            // Comprobamos que no nos salimos de la pantalla
            tmpFloat = (Float)finPuntos.elementAt( 0 );
            x1 = tmpFloat.floatValue();
            tmpFloat = (Float)finPuntos.elementAt( 1 );
            x2 = tmpFloat.floatValue();
            if( Math.round( x1*apAncho ) == Math.round( x2*apAncho ) )
                break;
            }
        }

    private void BorraSegmentos() {
        int indice = 0;
        int fin = finPuntos.size();

        for( int i=0; i < fin; i+=2 )
            {
            BorraTercioMedio( indice,indice+1 );
            indice += 4;
            }
        }

    private void BorraTercioMedio( int izqda,int dcha ) {
        float gap;
        float x1,x2;
        Float tmpFloat1,tmpFloat2;

        tmpFloat1 = (Float)finPuntos.elementAt( izqda );
        tmpFloat2 = (Float)finPuntos.elementAt( dcha );
        gap = tmpFloat2.floatValue() - tmpFloat1.floatValue();
        x1 = tmpFloat1.floatValue() + gap/3.0f;
        x2 = tmpFloat2.floatValue() - gap/3.0f;
        finPuntos.insertElementAt( new Float( x2 ),dcha ); 
        finPuntos.insertElementAt( new Float( x1 ),dcha ); 
        }
    }

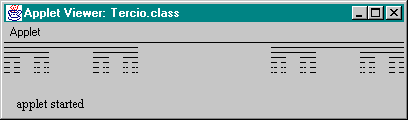
Aquí vemos el resultado de la ejecución del applet. ¿Está claro? Desde luego no es la representación más perfecta del conjunto, debido a que tenemos que manejar puntos de tamaño finito en lugar de puntos matemáticos genuinos. Dependiendo de lo larga que sea la ventana del applet, probablemente sólo se vean entre seis y doce interacciones antes de necesitar de que los pixels se vuelvan fraccionarios.

Es de hacer notar que en este programa Java hemos utilizado el objeto Vector. Debido a que Java no dispone de punteros, este objeto y la clase asociada, disponen de los métodos necesarios para poder implementar una lista enlazada, que es lo que nosotros hemos utilizado.

Tutorial de Java

[Anterior] [Indice] [Siguiente]