A través de líneas también se pueden realizar figuras más complicadas que resulten de la representación gráfica de funciones matemáticas. No pretendemos entrar en complicadas disquisiciones matemáticas, sino presentar algunas de las particularidades de los gráficos y Java. Vamos a presentar el código siguiente, Grafico1.java, que pintará la curva de la función seno de izquierda a derecha de la ventana:

import java.awt.*;
import java.applet.Applet;

public class Grafico1 extends Applet {
    int x0,xN,y0,yN;

    public void init() {
        Dimension d = size();

        x0 = y0 = 0;
        xN = d.width-1;
        yN = d.height-1;
        }

    public void paint( Graphics g ) {
        for( int x=x0; x < xN; x++ )
            g.drawLine( x,(int)(yN*Math.sin(x)),
                x+1,(int)(yN*Math.sin(x+1)) );
        }
    }

El corazón del funcionamiento del applet se encuentra en el bucle incluido en el método paint():

for( int x=x0; x < xN; x++ )
    g.drawLine( x,(int)(yN*Math.sin(x)),x+1,(int)(yN*Math.sin(x+1)));

El bucle va desplazándose a través de cada pixel de la pantalla en el eje x, y en cada una de las posiciones, calcula el seno para ese pixel. También calcula el seno del pixel siguiente y pinta una línea que une esos dos puntos. Debido a que el seno de un número real está siempre comprendido entre 1 y -1, escalamos el valor de y con yN. Y por fin hacemos un casting de los valores del seno en el eje y porque son flotantes fundamentalmente y el método drawLine() necesita enteros.

El applet anterior funciona correctamente, pero adolece de dos dos problemas: Primero, los senos son operaciones en coma flotante, luego para que el applet tenga realmente utilidad necesitamos utilizar números en coma flotante. Segundo, el sistema de coordenadas que maneja el applet va desde el punto (0,0), de la esquina superior-izquierda hasta la inferior-derecha. Pero el sistema normal de coordenadas Cartesianas empieza a contar desde la esquina inferior-izquierda. Lo que haremos será mover el origen al centro del applet y transformar las coordenadas del eje y para que vayan en las direcciones adecuadas.

La solución a los dos problemas anteriores puede tomar un montón de caminos diferentes, sin embargo, la clave se encuentra en separar los datos de lo que es la pantalla. Es decir, vamos a realizar nuestros cálculos matemáticos suponiendo que estamos en el espacio de un rectángulo en coordenadas cartesianas y, por otro lado, tomaremos a la pantalla como un rectángulo de puntos de ancho y tamaño fijos. Así podremos realizar los cálculos en el plano de los ejes cartesianos y presentarlos en el espacio reducido de la ventana del applet. Necesitaremos pues, un método para convertir un punto de la ventana del applet en un punto en el mundo cartesiano, y otro que haga la función contraria. El código siguiente, GraficoSeno.java, hace todo esto:

import java.awt.*;
import java.applet.Applet;

public class GraficoSeno extends Applet {
    int x0,xN,y0,yN;
    double xmin,xmax,ymin,ymax;
    int apAncho,apAlto;

    public void init() {
        Dimension d = size();
        apAncho = d.width;
        apAlto = d.height;

        x0 = y0 = 0;
        xN = apAncho-1;
        yN = apAlto-1;
        xmin = -10.0;
        xmax = 10.0;
        ymin = -1.0;
        ymax = 1.0;
        }

    public void paint( Graphics g ) {
        double x1,y1,x2,y2;
        int j1,j2;

        j1 = ValorY( 0 );
        for( int i=0; i < apAncho; i++ )
            {
            j2 = ValorY( i+1 );
            g.drawLine( i,j1,i+1,j2 );
            j1 = j2;
            }
        }

    private int ValorY( int valor ) {
        double x,y;
        int retorno;

        // Cartesianas equivalentes al punto de la pantalla
        x = (valor * (xmax-xmin) / (apAncho-1)) + xmin;
        // Calculamos el seno de ese punto
        y = Math.sin( x );
        // Escalamos la coordenada y dentro de los limites de la ventana
        retorno = (int)( (y-ymin) * (apAlto-1) / (ymax-ymin) );
        // Reconvertinos el valor cartesiano a punto de pantalla
        retorno = apAlto - retorno;

        return( retorno );
        }
    }

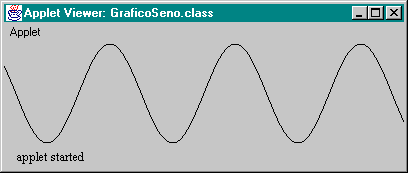
Ejecutando este applet, podremos observar que lo que se presenta ya se parece muchísimo más a la imagen que todos conocemos de la onda senoidal.

Tutorial de Java

[Anterior] [Indice] [Siguiente]