 Modeling bicubic patches
Modeling bicubic patches 
There are several kinds of parametric surfaces supported by 3D applications.
Bicubic patches are one of them and are supported by POV-Ray. Modeling bicubic_patch{} based objects using a text editor it's not an easy task. There are only two apps available for MacOS: PatchDance and D-form. Understanding a little of the math that behind bicubic patch computation it's very useful (and interesting), and will ease up the modeling. To keep things as easy as possible I start with the 2D case.
Cubic spline
The cubic spline it's a curve whose shape is controlled by four points that we can call "handles". I don't want to explain the full theory here, just the minimum to make you in condition to predict the shape of the spline just by looking at the handles.
Here's and example of a possible handle placement:
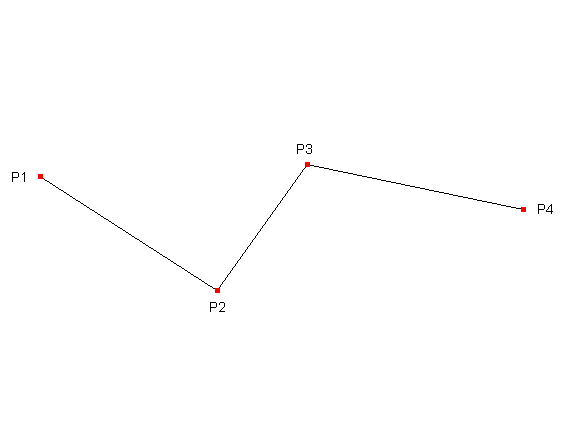
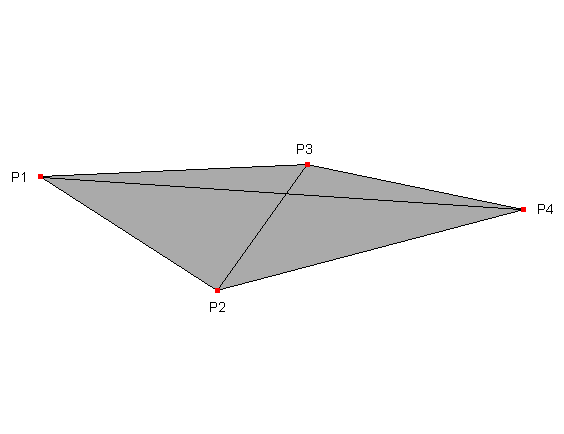
The first thing that we can say is that the curve will lay inside the minimum convex polygon that contains all the four handles. This polygon can be drawn by connecting each handle with each other. The outer boundaries forms the polygon:
Then let's discover that the curve in the point P1 is tangent to the segment P1-P2 and in the point P4 is tangent to the segment P3-P4. Add the fact that the curve tend to be as smooth as possible and that she "feels" the influence of P2 and P3 handles and you may draw by hand a scrap curve that, after a little exercise, will not look much different from the "real" shape. Here's how the curve will looks:
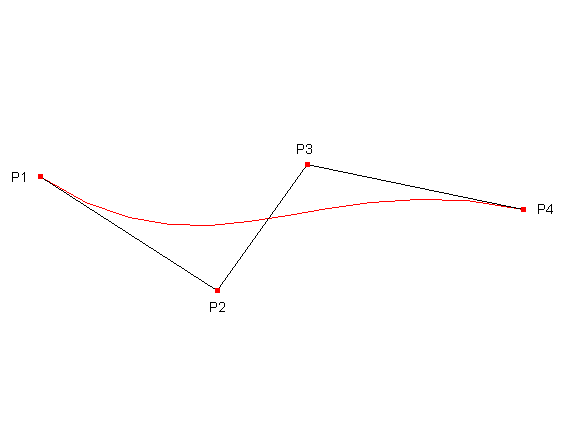
At this point you may want to play a little with a cubic spline editor to make some exercise.
D-form can help in this case. Although it doesn't provide cubic spline editing, we can fake it with a little trick.
Launch D-form and choose "Open - POV-Ray bicubic..." from the "File" menu. Open the file "patch.POV", than select "Perspective" from the "View" menu to switch perspective off (the option will became unchecked). Now select the "Top" view form "View" menu (or press command-5). Then select the Drag button on the left side of the window:

Et voila', here's a cubic spline editor!
To select and handle shift-click on it and than click and drag somewhere in the window to move it around. Shift-click somewhere in the white background to deselect all. (For complete explanation of D-form's features see the Docs).
Unlike most of you can think at this point, cubic splines are extremely powerful and easy to use tools. Let's face the fact that near all vector drawing apps like Freehand, Illustrator and Corel Draw! are based on this simple curve. Difficult to believe?
In such programs we are used to see a generic curve with a series of control points on it. When we click on one of these points two additional handles will appear. Let's examine the case of a curve with three of these control points (with all the additional handles displayed):
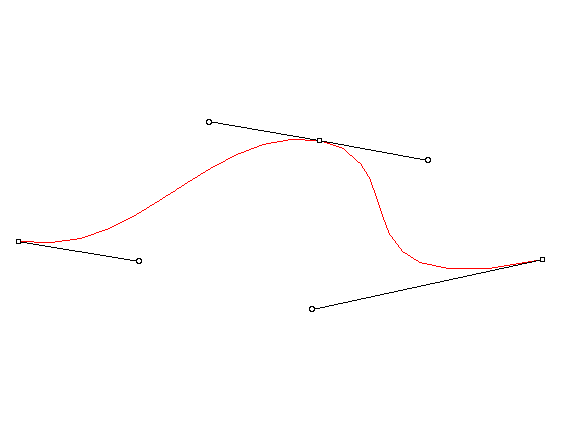
Well, this curve is nothing more than two cubic splines joined together:
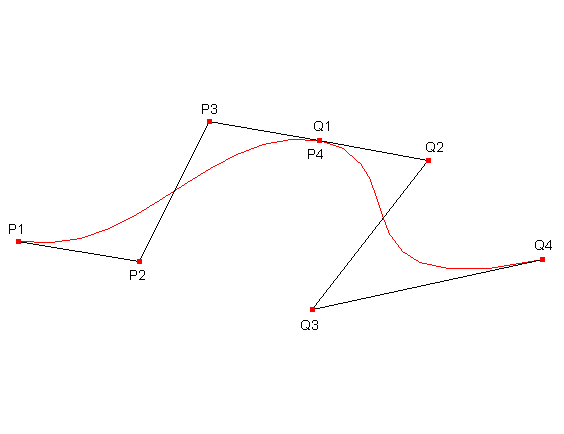
where P4 of the first curve and Q1 of the second one are coincident.
Pay attention to the fact that to ensure smooth connection between splines the segment that connect P3 handle of the first spline and Q2 of the second one must encounter the P4-Q1 junction. In all the drawing apps seen above when we move the P3 handle the P2 of the next spline must move in order to maintain smooth junction (unless we choose the option to make the control point P4-Q1 a "corner" point).
In D-form there is not such option and is up to you to maintain smooth connection between patches.
If we add a dimension to our world we will discover that cubic splines works even there. The four points lays now anywhere in the 3D space and the spline is now bounded by the object obtained by the usual method of connecting each vertex with every others. In this case the bounding object will be an irregular tetrahedron (eventually degenerated).
Bicubic patch
Bicubic patches are surfaces whose shape depends by sixteen handles. The handles can have any positions in the 3D space but usually we consider them disposed like a square matrix.
The resulting surface is a flat square. To understand what happens when we start to move the handles around let's notice that if we will consider four handles from one of the four rows or the four columns of the matrix we have a cubic spline. After we have drawn the eight splines we know that the surface "passes" by those splines. Like with cubic splines, making some exercise with patches will help learning.
In theory with bicubic patches it's possible to reproduce every shape, but in the real life things are not so easy. The main problem whit bicubic patches is that is difficult to maintain smooth continuity (and sometimes even continuity) across adjacent patches.
The typical approach is to start from an automatically generated shape like a sphere or a cylinder, and then deform the object paying attention to not loose smooth continuity. At this point I think the best thing to do is to download D-form and follow the tutorials I prepared.
If you have any problems or questions, please mail me.
Home > 3D Graphics > Persistence of Vision Raytracer > POV-Ray for MacOS Hints and Tips > Modeling bicubic patches
This page hosted by
 Get your own Free HomePage
Get your own Free HomePage





