 un modelo de autoorganización del cerebro - Tank y Hopfield- Lectura 20 -
un modelo de autoorganización del cerebro - Tank y Hopfield- Lectura 20 -
UN MODELO DE AUTOORGANIZACION DEL CEREBRO- El modelo de Hopfield del reemplazo de las neuronas por amplificadores operacionales analógicos alcanza, en principio, para explicar muchas propiedades trascendentes del cerebro de los animales avanzados, sobre todo algunas de la memoria asociativa e interpretación de la información (como el caso del perro de Pavlov que asocia sonido de campana con comida y segrega saliva). Los amplificadores operacionales analógicos, las resistencias, los condensadores y el cableado de Hopfield son dispositivos electrónicos. La computación colectiva que allí se logra se basa en Cada uno de ellos "vota" con (1) si hay descarga eléctrica y (-1) si no la hay. La tranquilidad o equilibrio se da cuando más negativos queden los amplificadores al final de la evolución: coincide con haber llegado a la mejor solución. E se mide por una expresión algebraica que incorpora un valor umbral de una pequeña carga positiva, por debajo del cual la neurona no dispara, aunque haya algo de tensión eléctrica positiva y tiene en cuenta todos los votos de todos los amplificadores. Mientras haya una solución mejor, la búsqueda no termina. La expresión para E tiene muy en cuenta que al final no haya discrepancia de votos entre los diversos amplificadores/neuronas. Tambien tiene en cuenta que el refuerzo del cable (aumento de V, el estímulo para la descarga o tambien el peso para efectuar ese recorrido) que deja pasar corriente continua, lleva a un valor menor de E, o sea más negativo. Todo esto se puede entender con un circuito biestable con dos amplificadores saturables. - Circuíto biestable o flip flop, con tomas a tierra batería -
resistencia para cada uno de los dos amplificadores operacionales. El
amplificador simula a una neurona y la toma a tierra simula a la membrana
de la neurona, por la cual se pierde actividad. (a) Cada amplificador
operacional de (b) se puede saturar con valores límite o asintóticos
cualquiera que sea la tensión de entrada de alguna de las dos maneras
indicadas por linea llena (normal, excitatriz) o de rayas (invertida,
inhibitoria). Esta última se usa en el ejemplo. (b) La evolución del
circuíto biestable depende del cociente entre los pesos de las resistencias
centrales. Los dos circulitos blancos Va y Vb son los sitios para
introducir las excitaciones externas o inputs. Los otros dos a la
izquierda son posiciones adicionales para el ingreso de corrientes. Los dos
llenos o negros son sitios usados para la medición de los potenciales Va y
Vb de output registrados en las graficas siguientes. (c) Si el proceso
recibiese Va = Vb a la entrada y tuviese iguales valores para las dos
resistencias centrales de (b), evolucionaría ya sea hacia (Va Vb) valiendo
(-1 +1) o bien a (+1 -1), los dos atractores existentes. La trayectoria
superior comienza con Va = Vb, puesto que esta sobre la diagonal que actua
de separatrix (lugar geometrico separador) entre ambos atractores. Se
orienta hacia uno de los atractores en lugar del otro por algun desbalance
circunstancial que no aparece explicito, pudiendo ser asimismo una
trayectoria hacia el otro atractor motivado por otro desbalance. La segunda [54]
trayectoria marcada se explica porque el punto inicial está del mismo lado
de la separatrix que el atractor. (d) Trayectoria en el caso cuando las
resistencias centrales de (b) son iguales. (e) Lo mismo, pero aquí
desiguales: desaparece la biestabilidad y pasa a haber un atractor único
asimétrico con rotura de la simetría previa. De un ordenamiento inicial
biestable (d) hubo una transición de fase hacia otro ordenamiento distinto
monoestable (e) causado por el cambio desde un cociente entre los pesos de
las resistencias centrales con valor, por ejemplo, 1, hacia otros valores
apartados. (Tank y Hopfield, Investigación y Ciencia, feb 1988, p. 47). La regla de Hebb señala que si las descargas entre dos neuronas son repetidas, algun mecanismo de crecimiento o cambio metabólico sucede a uno y otro lado de la hendidura sináptica, resultando como consecuencia un refuerzo que ayuda para que la segunda vez todo resulte más fácil y familiar. En 1982 esto significó una gran novedad. Las redes de este modelo pueden aprender. Pueden encontrar "relaciones en común" de ejemplos que se les proporcionan y generalizar esas relaciones en común para otras situaciones, como cualquier animalito con conducta pavloviana. Resumen de Tank y Hopfield, Investigación y Ciencia, feb. 1988, p.47 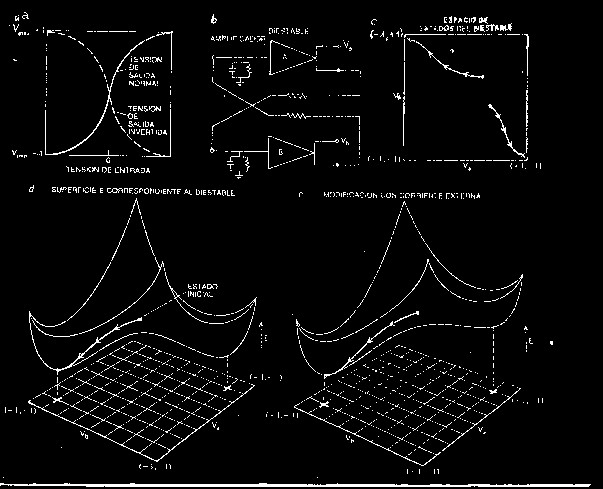
Cualquiera que sea el valor inicial para los dos estímulos para la descarga Va y Vb (zona de partida en el mapa), convergen a que si Va vale +1,Vb tenga que valer -1 y viceversa, si Vb vale +1, Va tenga que valer -1 (ver los dos atractores posibles del sistema biestable en la figura abajo y a la izquierda). Una vez que llegan a un atractor, se quedan en esa posición estable aunque haya perturbaciones amortiguadas. Alterando las condiciones iniciales de una situación simétrica (izquierda) a otra asimétrica (derecha) desaparece la biestabilidad y se establece una solución única o sea que aparece un atractor dominante. De todos modos las posibilidades finales son +1,-1 ó -1,+1, como se ve en la gráfica. Como muchas informaciones se pueden recodificar con expresiones binarias, esto implica recuerdo de cualquier información binaria, del tipo varón/mujer. Extendido a N amplificadores, donde todos se conectan entre sí, la red "neuronal" recuerda, aprende y distingue, evolucionando el circuito hacia el atractor de equilibrio. La dinámica se estabiliza con el logro de la mínima E, ver la tercera dimensión de la figura. Esto exige una actualización asincrónica de la información V de los N amplificadores, ya que si fuese sincrónica para todos, no opera correctamente. La clave del aprendizaje es que los pesos V similares a la intensidad de la sinapsis pueden ser aumentados de una manera incremental. ¿Cómo saben los pesos hacia dónde y cuánto cambiar? En los chips que aprenden son algoritmos (instrucciones matemáticas). En los animales son los mecanismos hebbianos y antihebbianos de alteración de neuronas con el aprendizaje.
6.dic.2000
Pulsar tecla de vuelta
Colección de lecturas de Biología- Carlos von der Becke.