Zurück
zum Inhaltsverzeichnis
Dipl.-Ing. Peter Fette; Am Schäferloch 16; D-75045 Walzbachtal /Germany
Zurück
zum Inhaltsverzeichnis
Kapitel 12
weiter zu Kapitel 14
Die Nutzarbeit der Maschine pro Umdrehung, wenn sie mit einem aus Gas und Sattdampf zusammengesetzten Arbeitsfluid arbeitet, ergibt sich aus der Nutzarbeit beider Einzelkomponenten abzüglich der Reibungsverluste.
(13.1)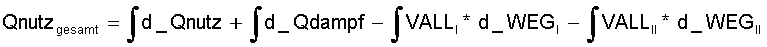 
mit d_Qnutz für die Gaskomponente nach Gl.(8.10) und d_Qdampf nach
Gl.(11.16); VALLI und VALLII sind die
Verlustkräfte an beiden Kurbeltrieben (siehe die Erläuterung zu
Gl.(13.16)). WEGI und WEGII sind die Wege der beiden Kolbenstangen.
Die gesamte zuzuführende Energie Qzugesamt ergibt sich für
die Gaskomponente aus der Integration von d_Qzu nach Gl.(10.2) und für
die Sattdampfkomponente aus der Summierung aller positiven Werte von
d_Qdampf aus Gl.(11.16). Rechnet man noch die Wiedererwärmung des Kondensats dazu,
dann ergibt sich Qzugesamt aus der Integration von d_Qzugesamt nach Gl.(12.3)
Der gesamte Wirkungsgrad ist dann nach Gl.(10.4):
(10.4)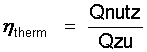 
Dieser gesamte Wirkungsgrad ist kleiner als der Wirkungsgrad für den Prozeß, wenn das Arbeitsfluid nur aus der Gaskomponente besteht. Die Erklärung dafür liefert Abb.7. Betrachtet man den idealen Stirling Prozeß für die Dampfkomponente -er entspricht dem "Rahmen" in Abb.7- dann erkennt man den enormen Unterschied in der isochoren Energieübertragung bei Vmin und dem isochoren Energieentzug bei Vmax. Bei nur Gas als Arbeitsfluid sind diese isochoren Energiebeträge betragsmäßig gleich, weil auch die Gasmasse während des Prozesses konstant bleibt. Sie werden bei einem 100% wirkenden Regenerator intern durch den Regenerator ausgeglichen.
Bei Sattdampf als Arbeitsfluid erhöht sich die Dampfmasse zunächst bei Vmin mit steigender Temperatur, dann erhöht sie sich weiter während der Expansion von Vmin auf Vmax. Somit muß wegen der erheblich größeren Dampfmasse bei Vmax auch erheblich mehr Kondensationswärme isochor von TE auf TC abgeführt werden, als Verdampfungsenergie bei Vmin isochor von TC auf TE aufgebracht werden muß.
Der Regenerator kann hier kaum wirksam werden; im theoretisch günstigsten Fall kann ein Regenerator gerade die Verdampfungsenergie, die bei Vmin aufgebracht werden muß, aus der erheblich größeren Kondensationsenergie bei Vmax beziehen. In Abb.14 verdeutlicht die gelb getönte Fläche den Energieverlust, der nicht durch den Regenerator bei Vmax ausgeglichen werden kann. Abb.14 ist ein T2-S2 Diagramm für den idealen Stirling Prozeß mit Gas + Sattdampf als Arbeitsfluid, wie auch der "Rahmen" in Abb.8.
Waehlen Sie den Zurueck Schalter Ihres Browsers, um an die vorherige Textstellen zurueck zu kommen
Kapitel 12
weiter zu Kapitel 14
Zurück zum Inhaltsverzeichnis