I. Korespondence s Paulem E. Blackem
2. dubna 1999
jsem poslal do fóra comp.programming a comp.theory mail Three Selection Algorithms:
Dobrý den,
mohli byste si přečíst můj článek FIND, SELECT, MODIFIND? (Česká verze je zde) Podívejte se na:
http://geocities.datacellar.net/SiliconValley/Garage/3323/3alg.html
Abstrakt:
Porovnávací studie tří algoritmů pro nalezení K-tého nejmenšího z N prvků:
Hoarova FINDu (H algoritmus);
mé modifikace FINDu (Z algoritmus);
Floydova a Rivestova SELECTu (FR algoritmus).
Závěr:
Algorithmy Z a FR jsou vždy lepší než H; FR provádí v průměru menší počet porovnání než Z;
Z provádí menší počet výměn než FR. Když počet výměn není kritický, je lepší FR než Z -
a naopak.
Paul E. Black mi napsal 6 dubna 1999:
Vážený dr. Zábrodský:
Četl jsem váš mail v comp.theory a váš článek "FIND, SELECT, MODIFIND" na mě udělal velký dojem. Byl jsem zvolen redaktorem Nového slovníku informatiky pro oblast algoritmy, datové struktury a problémy (Algorithms, Data Structures, and Problems of the new CRC Dictionary of Computer Science, Engineering and Technology)
http://hissa.nist.gov/dads/
Chtěl bych, aby tento sajt byl online referencí pro všechny, kdo se informatikou zabývají.
Hledám lidi, kteří by mi pomohli přidat hesla a definice do slovníku nebo je alespoň zkontrolovat.
Mohl byste přispět?
S úctou,
-paul-
--
Paul E. Black (p.black@acm.org) 100 Bureau Drive, Stop 8970
paul.black@nist.gov Gaithersburg, Maryland 20899-8970
voice: +1 301 975-4794 fax: +1 301 926-3696
Web: http://hissa.ncsl.nist.gov/~black/black.html KC7PKT
Odepsal jsem mu 12 dubna 1999:
Vážený dr. Blacku,
Mohu vám nabídnout:
1) Stručnou definici problému nalezení k-tého prvku:
Je dáno pole A obsahující N prvků a kladné celé číslo K <= N,
určete K-tý nejmenší prvek pole A a přerovnejte prvky pole tak, aby platilo:
A[1], A[2], ..., A[K-1] <= A[K] <= A[K+1], ..., A[N]
2) Implementaci N. Wirtha Hoarova FINDu v Pascalu (pro celočíselné pole X).
procedure FIND(K:integer);
var I,J,L,R,W,X:integer;
begin L:=1; R:=N;
while L<R do
begin X:=A[K]; I:=L; J:=R;
repeat
while A[I]<X do I:=I+1;
while X<A[J] do J:=J-1;
if I<=J then
begin W:=A[I]; A[I]:=A[J]; A[J]:=W;
I:=I+1; J:=J-1
end
until I>J;
if J<K then L:=I;
if K<I then R:=J
end
end
3) Moji implementaci algoritmu MODIFIND v Pascalu. Jde o jednoduché vylepšení
FINDu, které provádí menší počet výměn než FIND.
procedure MODIFIND(K:integer);
var I,J,L,R,W,X:integer;
begin L:=1; R:=N;
while L<R do
begin X:=A[K]; I:=L; J:=R;
repeat
while A[I]<X do I:=I+1;
while X<A[J] do J:=J-1;
W:=A[I]; A[I]:=A[J]; A[J]:=W;
I:=I+1; J:=J-1
until (J<K) or (K<I);
if J<K then L:=I;
if K<I then R:=J
end
end
-------------------------------------------------------------------------
Dále můžete použít kteroukoliv část mého článku "FIND, SELECT, MODIFIND".
S pozdravem
Vladimir Zabrodsky
A dr. Black mi obratem odpověděl (12. dubna 1999):
Vážený pane Zábrodský;
Děkuji za příspěvěk. Přidal jsem definice a algoritmy.
S úctou,
-paul-
II. Proč MODIFIND? Krátká historie mého algoritmu
S podivným chováním algoritmu FIND jsem se setkal poprvé v červnu roku 1989. Eliminoval jsem je jednoduchou úpravou algoritmu FIND. První program jsem napsal v Rexxu (měl 30 řádek), ale další průzkum jsem už prováděl pouze s implementací v Pascalu. V průběhu podzimu 1990 jsem napsal svůj článek Nalezení K-tého nejmenšího z N prvků, s pascalovskými verzemi programů, a poslal jsem jej do časopisu Bajt. Nebyl však ani po roce uveřejněn. Přepracoval jsem jej (rozšířil o nejhorší případ) a se svolením redakce časopisu Bajt jsem jej zaslal do časopisu Elektronika. V něm totiž od října 1991 vyšly už dva nebo tři příspěvky čtenářů právě na toto téma. Novou verzi článku jsem nazval Variace na klasické téma. Publikována byla v červnu, v 6. čísle za rok 1992. Ale v prosinci téhož roku, v 8. čísle Bajtu, vyšla překvapivě i moje původní verze. V obou článcích jsem Hoarův FIND nazýval P1 (zkratka první procedura v Pascalu) a moji modifikaci P2 (odolal jsem pokušení nazvat ji QUICKFIND). V mých poznámkách (tři školní sešity formátu A4, každý s 40-ti listy) označuji svůj algoritmus několikrát jako Fnd. V internetové (a Rexxové) verzi je prostě Z (Find je tam H a Select FR). Ovšem Z se mi nezdálo vhodné jméno pro slovník dr. Blacka a tak jsem ve svém mailu použil název MODIFIND ...
III. Poznámky k důkazu
Pro průměrný počet výměn u algoritmu MODIFIND uvádím odhad:
S(N, K) = 0.5((N + 1)HN
- (N - K)HN - K + 1
- (K - 1)HK)
|
Při výpočtu tohoto vzorce jsem postupoval stejně jako D. E. Knuth ve cvičeních 5.2.22 a dalších v [5]. Jak to, že jsem ale mohl použít stejný postup, když MODIFIND se chová jinak než Find? Podívejme se na následující příklad.
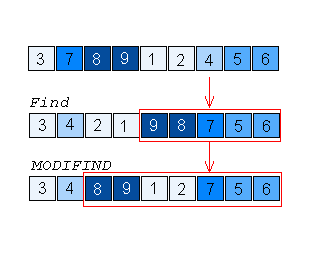
V prvním kroku Find odsune nalevo všechny prvky menší nebo rovny 4 a pokračuje v druhém kroku hledáním třetího nejmenšího prvku z pěti prvků 9, 8, 7, 5, 6.
MODIFIND přestane pracovat z číslem 4 v okamžiku, když zjistí, že to nemůže být sedmý nejmenší prvek. V druhém kroku bude hledat pátý nejmenší prvek v poli 8, 9, 1, 2, 7, 5, 6. Ale podívejte se dobře, přesun čísel 1 a 2 u Findu byl zbytečný. Tato čísla u MODIFINDu už v dalších krocích svou pozici nezmění! Z hlediska odhadu počtu výměn tedy můžeme u algoritmu MODIFIND předpokládat, že, stejně jako Find, v druhém kroku hledá třetí prvek v poli 8, 9, 7, 5, 6.
Průměrný počet výměn v prvním kroku jsem určil (na 17-ti stranách svých poznámek) jako:
((K - 1) (N - K) / 2N) + (N - 1) / N
Průměrný počet výměn pak je, s využitím návodu D. E. Knutha, dán vztahem:

IV. Stručná definice problému nalezení K-tého nejmenšího z N prvků
1. Předchozí definice
C. A. R. Hoare napsal v [1]:
Účelem programu Find je nalézt prvek pole A[1:N], jehož hodnota je podle velikosti f-tá v pořadí a přerovnat pole tak, aby tato hodnota byla v A[f] a dále, aby platilo, že všechny prvky s nižším indexem než f mají menší hodnotu a všechny prvky s vyšším indexem mají vyšší hoddnotu. Po skončení programu musí platit:
A[1], A[2], ... , A[f - 1] <= A[f] <= A[f + 1], ... , A[N]
V [2] R. W. Floyd a R. L. Rivest uvádí: Problém výběru ( Selection problem) může být stručně definován takto: je dána množina X n různých čísel a celé číslo i, 1 <= i <= n, má se určit i-tý nejmenší prvek X s co nejmenším možným počtem porovnání. Přitom i-tý nejmenší prvek, označme jej i o X, je takový prvek, který je větší než přesně i - 1 jiných prvků, takže 1 o X je nejmenší a n o X největší prvek v X.
V [3] R. W. Floyd a R. L. Rivest napsali: SELECT přerovná hodnoty prvků v segmentu pole X[L : R] tak, že X[K] (pro dané K; L <= K <= R) bude obsahovat (K - L + 1) nejmenší hodnotu, z L <= I <= K vyplývá X[I] <= X[K], a z K <= I <= R vyplývá X[I] >= X[K].
J.Bentley popsal problém nalezení K-tého nejmenšího prvku v článku [4] takto: Vstupem pro program SELECT je kladné celé číslo N, pole X[1 .. N], a kladné celé číslo K <= N. Program musí přerovnat prvky tak, aby platilo X[1 .. K - 1] <= X[K] <= X[K + 1 .. N]. Pak bude K-tý nejmenší prvek na pravém místě X[K].
Můj článek
FIND, SELECT, MODIFIND (česká verze je zde) obsahuje definici (cituji):
Problém nalezení K-tého nejmenšího z N prvků definoval C. A. R. Hoare v [1] takto: Je dáno pole A obsahující
N navzájem
různých prvků a celé čílo K, 1 <= K <= N, má se určit K-tý
nejmenší prvek A a pole se má přerovnat tak, aby prvek A[K] výsledného pole byl K-tým nejmenším prvkem a všechny prvky s indexem menším než K měly menší hodnotu a všechny prvky s indexem větším než K měly větší hodnotu. Musí tedy platit:
A[1], A[2], ..., A[K - 1] <= A[K] <= A[K + 1], ..., A[N]
|
2. Stručná definice problému výběru
Nejstručnější definice, která zohledňuje všechny dříve uvedené, zní:
Je dáno pole A obsahující N prvků a kladné celé číslo K <= N,
určete K-tý nejmenší prvek pole A a přerovnejte prvky pole tak, aby platilo:
A[1], A[2], ..., A[K - 1] <= A[K] <= A[K + 1], ..., A[N]
|
Literatura
1. C. A. R. Hoare: Proof of a Program: FIND CACM, r. 14,
č. 1, leden 1971, s. 39-45
2. R. W. Floyd, R. L. Rivest: Expected Time Bounds for Selection. CACM, březen 1975, r. 18, č. 3, s. 165-172
3. R. W. Floyd, R. L. Rivest: Algorithm 489 The Algorithm SELECT - for Finding the i-th
Smallest of n Elements [M1]CACM, březen 1975, r. 18, č. 3, p. 173
4. J. Bentley: Selection (in Programming Pearls) CACM, listopad 1985, r. 28, č. 11, s. 1121-1127
5. V. Zábrodský: Variace na klasické téma Elektronika, č. 6 1992, s. 33-34
6. V. Zábrodský: Nalezení k-tého nejmenšího prvku Bajt, č. 8 1992, s. 130-131
7. D. E. Knuth: The Art of Computer Programming. Sorting and Searching Addison-Wesley, Reading, Mass., 1973
|

