Интервал в СТО.
Назад: Параметр быстроты y, быстрота r.
Трехмерное пространство и время, сливаясь в один четырехмерный континуум, уже не является евклидовым четырехмерным пространством, но может быть отображено, как евклидово четырехмерное пространство. При этом метрические свойства самого пространства-времени и его отображения в евклидовом виде не совпадают. Поэтому пространство-время называют псевдоевклидовым пространством. В евклидовом пространстве, при переходе из одной системы координат в другую, сохраняется инвариантной величина r=(x2+y2+z2)1/2, которую мы можем назвать длина измерительного стержня, если величины x, y, z являются его проекциями на соответствующие оси координат. Длина такого стержня будет только положительной, и одной и той же в любой системе отсчета. Переходя от пространства к пространству-времени, мы теряем этот инвариант, но приобретаем другой: s=(x2+y2+z2-c2t2)1/2, который называют интервалом. Выбор знаков в этой записи (сигнатура) пока что не является общепринятым. Согласно нашему выбору сигнатуры, интервал s будет равен положительному числу, если r2=x2+y2+z2 больше c2t2. Такой интервал называется пространственноподобным. При этом можно найти такую систему отсчета, где разность времени между событиями, измеряемая нашим псевдоевклидовым четырехмерным стержнем, будет равна нулю. Это та система, где и измеряемый предмет, и четырехмерный измерительный стержень, покоятся друг относительно друга. Если r2 оказывается меньше, чем c2t2, то интервал будет времениподобным и будет равен некоторому мнимому числу. В разных системах координат, движущихся с разными скоростями относительно друг друга, величины r2 и c2t2 могут быть разными, но значение интервала будет одним и тем же. При этом можно найти такую систему отсчета, где пространственное расстояние r между событиями, измеряемое нашим четырехмерным стержнем, будет равно нулю. В этой системе отсчета он будет ориентирован параллельно её оси времени.
Знаки в записи квадрата интервала x2+y2+z2-c2t2 можно сделать одинаковыми, вводя вектора двух сортов: ковариантные и контравариантные, либо вводя мнимую единицу i=(-1)1/2.
s2=x2+y2+z2+(ict)2.
Но от этого пространство-время не становится евклидовым, а остается псевдоевклидовым. Для удобства координатных построений отбрасывают пару пространственных координат, а на чертежах оставляют ось x и ict. Измеряя линейкой расстояние между какими-нибудь двумя точками на комплексном чертеже, мы получаем модуль комплексного числа, (r2+(ct)2)1/2, а эта величина не равна интервалу, (r2+(ict)2)1/2=(r2-(ct)2)1/2. Модуль комплексного числа получают извлечением корня из произведения комплексного числа x+iy на комплексно сопряженное число x-iy. Квадрат интервала напоминает скалярное произведение вектора самого на себя. Как же тогда измерить интервал? Это ведь все равно, что пытаться измерить линейкой расстояние между сегодняшней тумбочкой и вчерашним углом стола. Как ни крути линейку, а до вчерашнего стола ты уже не дотянешься. Но этот интервал все же можно измерить. Линейкой меряем пространственное расстояние, а по часам отсчитываем временной промежуток. Подставляем в формулу (r2-(ct)2)1/2, и получаем значение интервала. Точно также и на комплексном чертеже: измеряем по отдельности и x, и ict линейкой. Далее проводим вычисления и видим, что интервал s может быть как положительным числом, так и чисто мнимым, а квадрат интервала s2 будет положительным, или отрицательным. Величина (r2+(ct)2)1/2 может быть названа модулем R радиус-вектора R=(r, ict), а далее использоваться для представления комплексного числа в тригонометрической и показательной формах:
R = (r, ict) - алгебраическая форма;
R = R·(cosj, i·sinj) - тригонометрическая форма;
R = R·exp(ij) - показательная форма.
Иногда вместо запятой в формах записи ставят знак плюс, но комплексное число это одна точка в комплексной плоскости, а не сумма чисел.
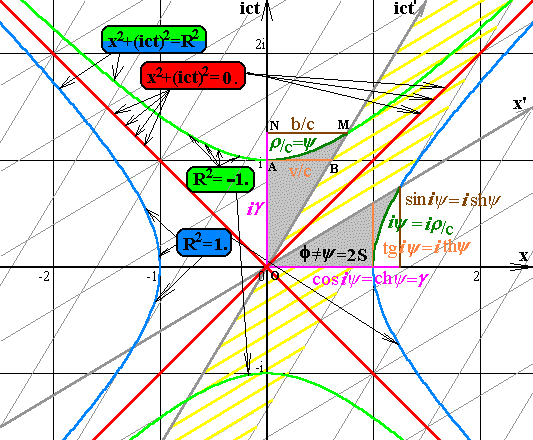
Рис. 2. Псевдоевклидова окружность. Эта псевдоокружность терпит разрыв в четырех точках. Квадрат интервала и сам интервал между центром рисунка и любой точкой правой или левой гиперболы равен единице. Квадрат интервала между центром рисунка и любой точкой верхней или нижней гиперболы равен минус единице, а интервал равен мнимой единице i. Интервал от центра рисунка до любой точки асимптот, показанных красным цветом, равен нулю. К этому рисунку мы вернемся на странице 9, а потом увидим, что здесь на самом деле здесь две псевдоокружности, и что на них живут частицы...
Дальше: Четырехмерные скорости.
Назад: Параметр быстроты y,
быстрота r.
К оглавлению раздела Некоторые вопросы СТО.
К другим разделам Космической Генетики.
Последнее обновление страницы: 24 апреля 2007 года.
|
Экстренная вставка, 2009. Внимание! Магнитный капкан Дьявола!Наша Земля уже могла быть взорвана 21 сентября 2008 года, но за два дня до первых столкновений коллайдер вышел из строя. На повторное везение не рассчитывайте. Действуйте! Что нам даст LHC: частицу Бога, или магнитный капкан Дьявола?
Новости, ссылки, сбор средств на создание Живого Щита. Конец экстренной вставки, 2009.
|
Из Википедии.
[1] 4-векторы впервые рассмотрели Пуанкаре (1905) и затем Минковский. Они рассматривали временную компоненту 4-вектора чисто мнимой, что автоматически порождало нужное правило вычисления скалярного произведения при обычном суммировании произведений компонент.
4-вектором (четырёхвектором, четыре-вектором) называется вектор в четырёхмерном пространстве вещественных чисел. Координаты 4-вектора при переносе или повороте системы отсчёта преобразуются как соответствующие им координаты в пространстве Минковского. В 4-векторе одна временная компонента и три пространственных.
В современных обозначениях временной компоненте обычно соответствует индекс 0 (то есть она считается нулевой компонентой), пространственным: 1,2,3 — совпадающим с x, y, z (обычно, по умолчанию и если возможно, это обычные прямоугольные декартовы координаты). В старой литературе часто используется соглашение (восходящее к Минковскому), по которому временная компонента считалась не нулевой, а четвёртой.
Иногда бывает удобно приписывать временной компоненте 4-вектора чисто мнимый характер (всегда умножать действительную временную компоненту на мнимую единицу). Такое представление 4-векторов было исторически введено первым, однако не слишком редко — в силу своего удобства — используется и в современной литературе.
4-векторы (их компонентное представление) могут быть записаны в контравариантной и (или) ковариантной форме (см. ниже), которые не всегда совпадают, а в случае действительного представления (без мнимой единицы) всегда различаются между собой...
Скалярные произведения (в частности, квадраты) 4-векторов вычисляются с использованием метрики Лоренца.
Они инвариантны относительно преобразований Лоренца. Они называются скалярами (в четырёхмерном — пространственно-временном — смысле).
Например, это интервал (квадрат интервала есть квадрат вектора перемещения в метрике Лоренца), масса (масса покоя) — её квадрат есть, с точностью до постоянного множителя, квадрат 4-импульса: m2 = E2 / c4 − p2 / c2 и т. д.