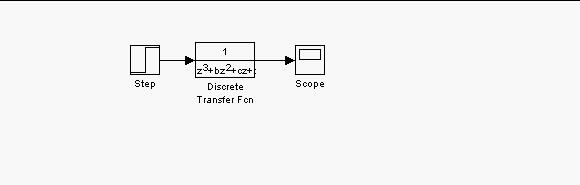
Digital Controller
The closed loop transfer function from the State Variable Feedback Controller is:
num/den =
-4.263e-014 s^3 - 1.364e-012 s^2 - 2.183e-011 s - 1
---------------------------------------------------
s^4 + 50 s^3 + 1056 s^2 + 1.107e+004 s + 5.091e+004
After a conversion to the z-domain using the c2d function we obtain the z-transform:
-7.97e-007 z^4 - 3.188e-006 z^3 - 4.782e-006 z^2 - 3.188e-006 z - 7.97e-007
---------------------------------------------------------------------------
z^4 - 0.6324 z^3 + 0.3352 z^2 - 0.06315 z + 0.009482
To facillitate the sampling of the continuous system, I used coefficients (a,b,c,d,e,f,g,h,i) to represent the coefficients I obtained from the z-transform.
a = 0.6324; b = -0.3352; c = 0.06315; d = -0.009482; e = -7.97e-007; f = -3.188e-006; g = -4.782e-006;
h = -3.188e-006; i = -7.97e-007;
In order to get the transfer function in to a form to discretize it, one needs to divide through by the highest order and solve for the difference equation in the time-domain:
Yk = a*yk-1 + b*yk-2 + c*yk-3 + d*yk-4 + i*uk + h*uk-1 + g*uk-2 + f*uk-3 + e*uk-4;
Below is the simulink model and the matlab code which simulates the digital controller, Along with the plots for the continuous system and the digital system versus time.

%Project #1
%Ball Balancer
%State Variable Feedback Method
clear all;
global A;
global B;
global K;
global m; % mass of ball
global g; % gravity
global pn; % nominal point
global J; % inertia of the beam
% Set Parameter Values
m=1;
g=9.81;
pn=1;
J=8.81;
%state space matrices
A=[0 1 0 0; 0 0 -g 0; 0 0 0 1; (-m*g)/(m*pn^2+J) 0 0 0];
B=[0; 0; 0; 1/(m*pn^2+J)];
%C=[1 0 0 0; 0 0 1 0];
C=[1 0 0 0];
D=[0];
[num,den] = ss2tf(A,B,C,D);
[numc,denc] = cloop(num,den);
%Ackerman Method
POV = 4;
ts = 0.5;
alpha = 5/ts;
zeta = 0.716;
wn = alpha/zeta;
deltaD= [1 2*alpha wn^2];
%p = roots(deltaD)
%[Q,R]= deconv(denc,deltaD);
Q = [1 30 261]; % s = -15 +/- j6
deltaC = conv(deltaD,Q);
p = roots(deltaC);
K = acker(A,B,p);
% check the design by computing closed loop poles
Ac = A-B*K;
[numC,denC] = ss2tf(Ac,B,C,D);
% see if denC and deltaC are the same to check design
%Discretization
[numc,denC]=cloop(numC,denC,-1);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% converting the controller using the BLT to a digital controller
T = 0.1;
printsys(numC,denC,'s')
csys = tf(numC, denC)
dsys = c2d(csys, T, 'tustin')
%Transfer function:
%-7.97e-007 z^4 - 3.188e-006 z^3 - 4.782e-006 z^2 - 3.188e-006 z - 7.97e-007
%---------------------------------------------------------------------------
% z^4 - 0.6324 z^3 + 0.3352 z^2 - 0.06315 z + 0.009482
a = 0.6324;
b = -0.3352;
c = 0.06315;
d = -0.009482;
e = -7.97e-007;
f = -3.188e-006;
g = -4.782e-006;
h = -3.188e-006;
i = -7.97e-007;
% Following loop shows discrete sequences for the responses
for k = 1:100
y(k) = 0;
u(k) = 0;
end
for k = 10:100
u(k) = 1;
y(k) = a*y(k-1) + b*y(k-2) + c*y(k-3) + d*y(k-4) + i*u(k) + h*u(k-1) + g*u(k-2) + f*u(k-3) + e*u(k-4);
%y(k) = y(k) + d*y(k-4) + i*u(k) + h*u(k-1);
%y(k) = y(k) + g*u(k-2) + f*u(k-3) + e*u(k-4);
end
q = [1:40];
e = [1:40];
for k = 1:40
q(k) = y(k+9);
e(k) = 1-y(k+9);
end
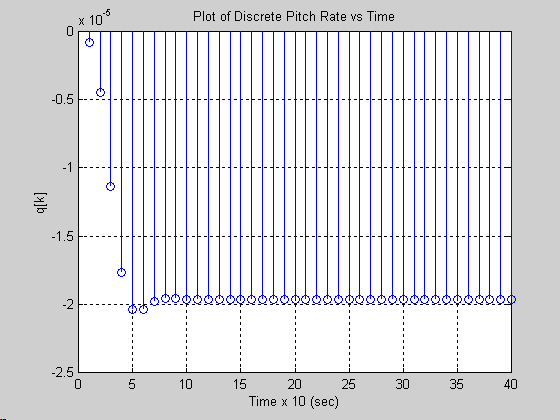
stem(q)
grid
title('Plot of Discrete Pitch Rate vs Time')
ylabel('q[k]')
xlabel('Time x 10 (sec)')
%pause
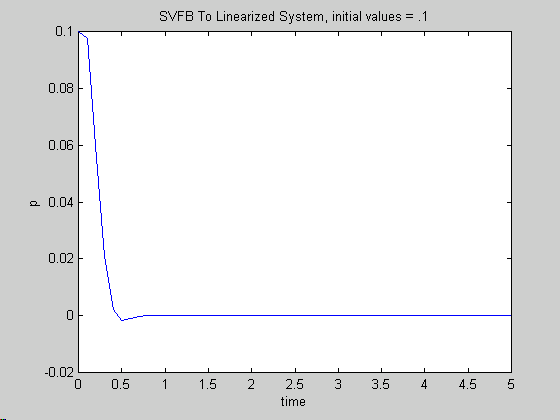
Linearize Non-linear Equations