#10
Analysis Of Normal-Appearing White Matter In Multiple Sclerosis: Comparison Of Diffusion Tensor MR Imaging And Magnetization Transfer Imaging
Background And Purpose
Our purpose was to compare Diffusion Tensor MR and Magnetization Transfer imaging in assessing Normal-Appearing White Matter (NAWM) regions in Multiple Sclerosis (MS).
Methods
Diffusion Tensor, Magnetization Transfer, and conventional MR imaging were performed in 12 patients with MS.
Fractional Anisotropy, Apparent Diffusion Coefficients (ADCs), and Magnetization Transfer Ratios (MTRs) were measured in plaques, Normal-Appearing PeriPlaque WM (PWM) regions, and Normal-Appearing WM regions remote from plaques.
Mean Fractional Anisotropy, ADCs, and MTRs were calculated and compared in WM regions.
Results
Fractional Anisotropy was lower in Normal-Appearing PWM regions than in remote WM regions (P < .001) but higher than in plaques (P < .001).
MTRs were lower (not significantly, P =.19) in Normal-Appearing PWM regions than in remote regions. MTRs were higher in Normal-Appearing PWM regions than in Plaques (P < .001).
ADCs were higher in Normal-Appearing PWM regions than in remote regions (P =.008) but lower than in Plaques (P =.001).
Correlation between Fractional Anisotropy and MTRs of individual Lesions was poor (r = 0.18) and between Fractional Anisotropy and ADC, modest (r = -0.39).
Conclusion
In MS, Diffusion Tensor MR imaging can depict differences between WM regions that are not apparent on conventional MR images.
Anisotropy measurements may be more sensitive than those of MTRs in detecting subtle abnormalities in PWM.
#11
Cercignani M, Bozzali M, Iannucci G, Comi G, Filippi M
J Neurol 2002 Jul;249(7):875-83
Scientific Institute and University, Ospedale San Raffaele, NeuroImaging Research Unit, Dept. of NeuroScience, via Olgettina 60, 20132 Milan, Italy
PMID# 12140672; UI# 22135914
Abstract
Previous Diffusion Tensor Magnetic Resonance Imaging (DT-MRI) studies reported Mean Diffusivity (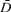 >) and Fractional Anisotropy (FA) changes in lesions and Normal-Appearing White Matter (NAWM) of patients with Multiple Sclerosis (MS). >) and Fractional Anisotropy (FA) changes in lesions and Normal-Appearing White Matter (NAWM) of patients with Multiple Sclerosis (MS).
But, neglected the additional information which can be obtained by the analysis of the Inter-Voxel Coherence (C).
The present study is based on a large sample of patients with MS and it is aimed at assessing the potential role of C in the quantification of MS-related tissue damage of T2-visible lesions and NAWM.
We obtained dual-echo, T1-weighted and DT-MRI scans from 78 patients with Relapsing/Remitting (RR), Secondary/Progressive (SP), or Primary/Progressive (PP) MS and from 26 healthy volunteers.
We calculated 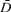 , FA and C of T2-HyperIntense lesions, T1-IsoIntense lesions, T1-HypoIntense lesions and several areas of the NAWM. , FA and C of T2-HyperIntense lesions, T1-IsoIntense lesions, T1-HypoIntense lesions and several areas of the NAWM.
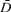 and FA of the majority of NAWM regions studied from MS patients were different from the corresponding quantities of the White Matter from controls. and FA of the majority of NAWM regions studied from MS patients were different from the corresponding quantities of the White Matter from controls.
NAWM C from patients was lower than White Matter C from controls only for the Parietal PeriCallosal Areas.
SPMS patients had higher Corpus Callosum 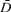 and lower Corpus Callosum FA and C than patients with either RRMS or PPMS. and lower Corpus Callosum FA and C than patients with either RRMS or PPMS.
Average lesion 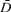 was higher, and average FA and C lower than the corresponding quantities measured in the NAWM. was higher, and average FA and C lower than the corresponding quantities measured in the NAWM.
Average T1-HypoIntense lesion 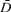 was higher and average FA lower than the corresponding quantities of T1-IsoIntense lesions, whereas average C of these two lesion populations were not different. was higher and average FA lower than the corresponding quantities of T1-IsoIntense lesions, whereas average C of these two lesion populations were not different.
SPMS had higher average lesion 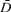 than both PPMS and RRMS patients. than both PPMS and RRMS patients.
NAWM 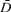 and C of the Corpus Callosum were moderately correlated with disability. and C of the Corpus Callosum were moderately correlated with disability.
This study confirms the role of DT-MRI metrics to identify MS lesions with different amounts of tissue damage and to detect diffuse changes in the NAWM.
It also shows that measuring C enables us to obtain additional information about tissue damage, which is complementary to that given by the analysis of 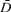 and FA. and FA.
#12
A Normal Distribution For Tensor-Valued Random Variables: Applications To Diffusion Tensor MRI
Basser PJ, Pajevic S
IEEE Trans Med Imaging 2003 Jul;22(7):785-94
STBB/LIMB/NICHD, National Institutes of Health, Bldg. 13, Rm. 3W 16, 13 South Drive, Bethesda, MD 20892-5772, USA
PMID# 12906233
Abstract
Diffusion Tensor Magnetic Resonance Imaging (DT-MRI) provides a statistical estimate of a symmetric, second-order Diffusion Tensor of water, D, in each Voxel within an imaging volume.
We propose a new normal distribution, p(D) alpha exp(-1/2 D: A: D), which describes the variability of D in an ideal DT-MRI experiment. The scalar invariant, D : A : D, is the contraction of a positive definite symmetric, fourth-order precision Tensor, A, and D.
A correspondence is established between D: A: D and the elastic strain energy density function in continuum mechanics - specifically between D and the second-order infinitesimal strain Tensor, and between A and the fourth-order Tensor of elastic coefficients.
We show that A can be further classified according to different classical Elastic Symmetries (i.e., Isotropy, Transverse Isotropy, Orthotropy, Planar Symmetry, and Anisotropy).
When A is an Isotropic fourth-order Tensor, we derive an explicit analytic expression for p(D), and for the distribution of the three eigenvalues of D, p(gamma1, gamma2, gamma3), which are confirmed by Monte Carlo simulations.
We show how A can be estimated from either real or synthetic DT-MRI data for any given experimental design. Here we propose a new criterion for an optimal experimental design: that A be an Isotropic fourth-order tensor.
This condition ensures that the statistical properties of D (and quantities derived from it) are rotationally invariant. We also investigate the degree of Isotropy of several DT-MRI experimental designs.
Finally, we show that the univariate and multivariate distributions are special cases of the more general Tensor-variate normal distribution, and suggest how to generalize p(D) to treat normal random Tensor variables that are of third- (or higher) order.
We expect that this new distribution, p(D), should be useful in feature extraction; in developing a hypothesis testing framework for segmenting and classifying noisy, discrete Tensor data; and in designing experiments to measure Tensor quantities.
|