The Adaline is the next neural network we will examine. Adaline stands for ADaptive LInear NEuron. Just as with the McCulloch-Pitts Neuron, the adaline is not a neural network by itself. However when connected with input nodes, it does form a network. The adaline, just like the perceptron, uses a training algorithm that was developed mathematically rather than biologically. This training algorithm, the delta rule, is a very powerful training algorithm and was in fact extended later for another neural network to form one of the most powerful training algorithms. Fortunately the proof for the delta rule is fairly simple, so we can examine why the delta rule works as a training algorithm.
The architecture for the adaline is rather simple. It is a two layer network (single if we ignore the input layer) with an optional bias on the output layer. The input nodes use the identity function for their activation function and the output nodes use a binary, bipolar, or some other form of a threshold function.
The thing we wish to focus on when talking
about the adaline is its training algorithm, the delta rule. The
idea behind the delta rule is to minimize the difference between
the desired output and actual output produced by the network. In
order to minimize this difference, the error for a particular
pattern, we need to develop a mathematical expression to
represent this error. Before jumping to conclusions and using the
difference between the target and actual output values for the
error, we must analyze the situation. Since the network can have
multiple outputs, in order to have a single error for a
particular training pattern, we will need to sum the errors at
each individual output node. Mathematically this can be
represented by the formula, ![]() where m is the number of output nodes and Ej
is the error at output node j. Now an expression
for the error at output node j is necessary. The error can
be defined as the difference between the target value and actual
output value, as was originally stated. But this will cause
problems when the error is being summed. Since some errors may be
positive and others negative, when they are added up, the total
error will not give an accurate representation of the magnitude
of the real error. In order to make all the errors at the output
nodes positive, the difference between the target value and
output value is squared. Unfortunately, since the activation
function used is not differentiable, we must use the net input to
the output node instead of the activation of the output node.
Thus the final error function is given in figure 12.
where m is the number of output nodes and Ej
is the error at output node j. Now an expression
for the error at output node j is necessary. The error can
be defined as the difference between the target value and actual
output value, as was originally stated. But this will cause
problems when the error is being summed. Since some errors may be
positive and others negative, when they are added up, the total
error will not give an accurate representation of the magnitude
of the real error. In order to make all the errors at the output
nodes positive, the difference between the target value and
output value is squared. Unfortunately, since the activation
function used is not differentiable, we must use the net input to
the output node instead of the activation of the output node.
Thus the final error function is given in figure 12.
![]()
The goal of the delta rule is to find a set of weights such that this error is minimized. We need to figure out whether the weight on a particular connection should be increased or decreased from its current value to decrease the error. We can accomplish this by taking the partial derivative of the error function with respect to the weight we are changing.
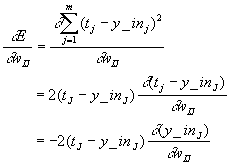
If the net input to an output node, y_inj,
is represented mathematically you get the expression.![]() . Consequently,
. Consequently,
![]()
The sign of the partial derivative tells the direction we should change wIJ to increase the error. Since we wish to decrease the error we should change wIJ in the opposite direction. Since the partial derivative tells us nothing about how far to change the weight, we need to introduce a learning rate constant that says what fraction of the partial derivative we should move. Therefore the change in the weight can be expressed by the following expression.
![]()
Believe it or not, we have just derived the delta rule. Because the rule is commonly left in the form shown in figure 13, the rule is called the delta (D ) rule. Instead of giving the new weights, the delta rule tells us the change in the weights. To find the new weights, add the value obtained by evaluating the delta rule to the existing weight along the connection. We have encountered all the variables in the expression for the delta rule before. Just to refresh your memory, a is the learning rate constant, tJ is the desired output for node J, y_inJ is the input to the output node J, and xI is the output from input node I.
Training a neural network using the delta rule is similar to the training procedure for the perceptron. After applying an input pattern, the weight changes are calculated at all the output nodes. The weights are then updated and continue feeding the neural network training patterns. Once an epoch is completed, you sum the errors from all the individual training patterns. If the error is acceptable, the training stops, otherwise you repeat the process using the same set of training patterns.
![]()
Home Page ![]() Introduction
Introduction ![]() Biological Neural Networks
Biological Neural Networks ![]() McCulloch-Pitts Neuron
McCulloch-Pitts Neuron
Perceptron ![]() Adaline
Adaline ![]() Back Propagation network
Back Propagation network
References ![]() Research Paper
Research Paper ![]() Glossary
Glossary
![]() Beware:
This page is always under construction
Beware:
This page is always under construction
![]() Geocities
Geocities
![]() Geocities
Research Triangle
Geocities
Research Triangle