The first thing that must be addressed is the question, "What is a neural network?". Since there are many different types of networks, and each type has great similarites as well as significant differences in comparison to other types, the answer to this question is a difficult one. I think the best answer was given by Maureen Caudill and Charles Butler in their book, Understanding Neural Networks (see References).
A neural network is an information processing system that is nonalgorithmic, nondigital, and intensely parallel. It is not a computer in the sense we think of them today, nor is it programmed like a computer. Instead, it consists of a number of very simple and highly interconnected processors called neurodes, which are the analogs of the biological neural cells, or neurons, in the brain.
This definition, when broken down, addresses each important general concept about artificial neural networks. Before I pick apart the definition, let me clarify what it is a definition of. Although we were seeking a defintion for a neural network, I gave you the authors definition of an artificial neural network. What's the difference, you ask. Simple. An artificial neural network, is the man-made equivalent of a biological neural network. The details of biological neural networks will be discussed in the next section, but for now just remember that the designs for the early artificial networks and the designs for some of the later ones were based on the most amazing biological network, the human brain. Now lets analyze the definition for artificial neural networks.
First artificial neural networks (neural nets for short) are nonalgorithmic. Mainstream computer programming relies on the concept of an algorithm to instruct computers. This algorithm, when placed in some computer language, a program, instructs the computer step-by-step how to accomplish a particular task. The task, which can range from computing a complex mathematical expression to downloading e-mail from the internet, is accomplished by following the steps in the computer program. During the process, if the program encounters something unexpected, chances are the program will crash unless the programmer forsaw the occurence. Conversely, neural nets don't use algorithms, or at least not in the same sense as a traditional computer program. Neural nets 'learn' how to accomplish a particular task. That's right, they learn. Each neural network architecture has its own training algorithm associated with it, but there are two primary methods of training. The first, supervised training, is akin to teaching a little kid by example. You give the neural network the input and the corresponding correct output, and the network tries to figure out the relationship between the input and the output. The second method, self-organization or unsupervised training, allows the neural net to separate a set of training input patterns into various categories based on the similarities and differences between the inputs.
Second, neural networks are nondigital. This simply means that neural nets are not restricted to giving binary (1's and 0's) output and taking binary input. Depending on the architecture, neural networks can give binary output, bipolar output (-1 or 1), or output corresponding to values of any differentiable curve.
Third, neural networks are intensely parallel. The idea behind most neural network designs is to have processing occur simultaneously (in parallel) at each individual processing unit. Unfortunately when implemented using a typical computer, this feature of neural networks is taken away because of the limitations of hardware. However, if special equipment is being used to implement a neural network, it is generally done with individual processing elements so that the network will run in parallel.
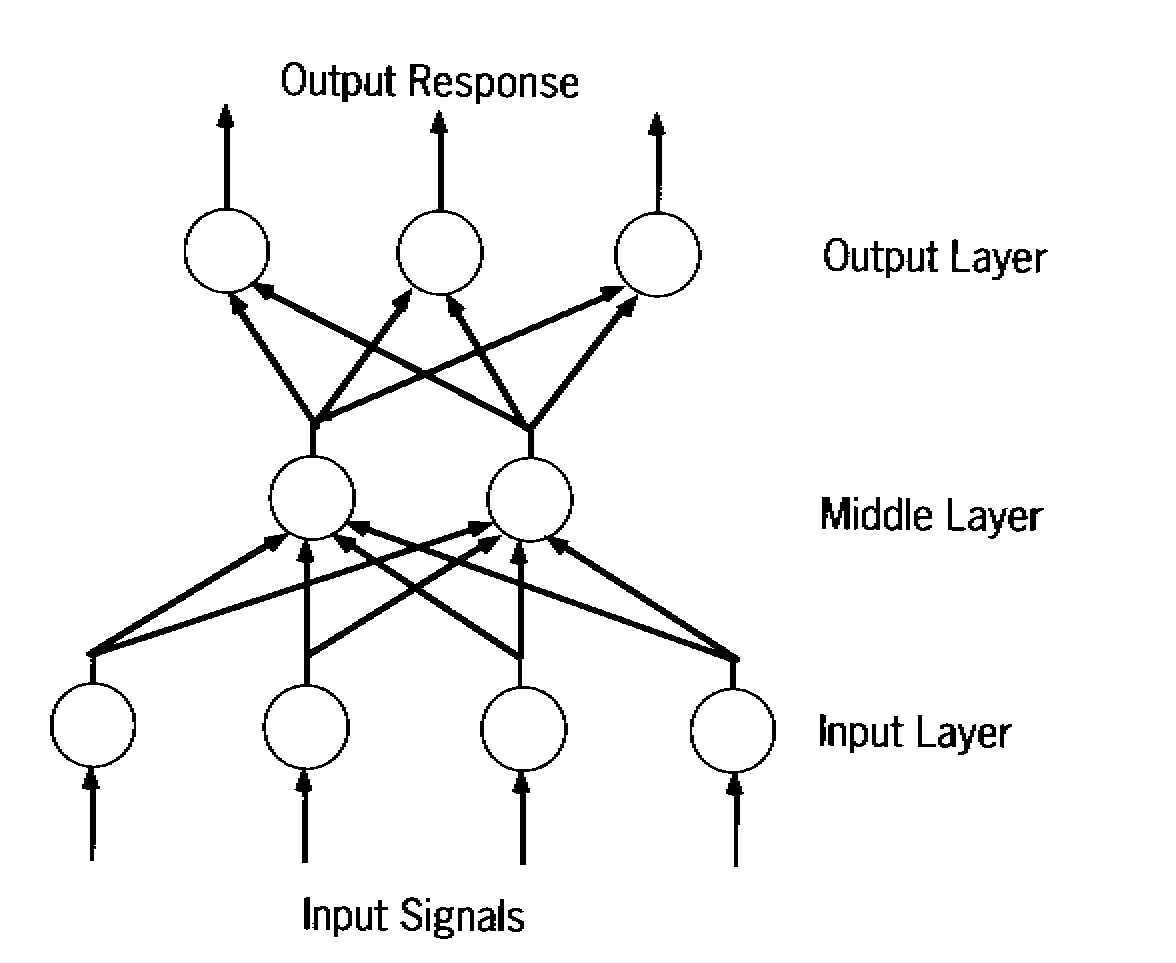
Fourth, and by far most important, neural networks consist of a number of very simple and highly interconnected processors called neurodes. As the definiton states, neurodes are the analogs of biological neurons. Neurodes are also known as nodes or sometimes even neurons. Generally speaking, nodes within all neural networks follow a common model of operation. They sum their input signals, pass the summed value through an activation function, and send that value out as its output signal. This output signal will either leave the network or will travel along a connection to another node, and act as an input to that node. As signals pass from node to node along the interconnections, the signal is scaled (multiplied) by a weight associated with that connection.
All the neural networks that are discussed on this site have their nodes arranged in layers. When a network has its nodes arranged in this way, every node on a particular layer (excluding the input layer) receives input from every node on the previous layer, and sends output to every node on the next layer.
Lets discuss the operation of neural networks. As was stated earlier, each node sums its input signals, pass the summed value through an activation function, and output the resulting value. Generally, input nodes use the identity function, where output is equal to the input, as their activation function. Consequently, the output of a input node is equal to its single input. Because of this property, input nodes and the input layer are often ignored when dealing with neural networks. Each middle node, takes the weighted sum of the output signals from the input nodes and passes it through its activation function. Output nodes repeat the process except they use the output signals from the middle(hidden) nodes as opposed to the signals from the input nodes. The net input and output signal of any particular node (except input nodes) in a neural network can be represented by the following mathematical formula.
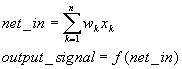
That's basically all you need to know to begin exploring specific neural network architectures. Before that, I would like to discuss the notation that will be used during the explanations of the neural network architectures and learning rules.
Home Page 
Introduction Biological Neural
Networks
McCulloch-Pitts Neuron
Perceptron Adaline Back Propagation
network
References Research Paper Glossary
Beware: This
page is always under construction
Geocities
Geocities
Research Triangle