The McCulloch-Pitts neuron is really not a neural network. It is a model for nodes that make up a neural network. However in combination with the input nodes, the McCulloch-Pitts neuron does indeed form a neural network. Although this is a very basic network, it shares many of the same features as the complex neural networks that follow it, but lacks one of the key features, a training algorithm.

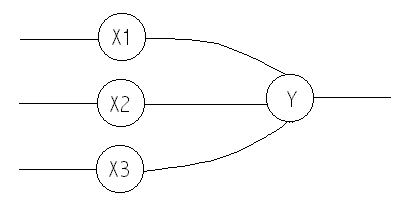
Node Y in this figure represents a McCulloch-Pitts Neuron
A McCulloch-Pitts neuron is a single node that receives input from weighted links. The weights can be positive (excitatory) or negative (inhibitory). All excitatory weights are equal, and all inhibitory weights are equal. The input signals and activation for a McCulloch-Pitts neuron are binary. That is, they may have values of either one or zero. The activation function for a McCulloch-Pitts Neuron is a threshold function similar to the one discussed earlier.
![]()
The threshold for the McCulloch-Pitts neuron, theta , must be set such that if there are any inhibitory input signals, the activation of the node must be zero.
A McCulloch-Pitts neuron can have any number of inputs. For convenience let us say there are n excitatory inputs and m inhibitory inputs. The architecture dictates that all excitatory inputs have the same incoming weight. We will call this weight w where w>0. Similarly all inhibitory weights, we’ll call them -p where p>0, must be equal. Since the activation function for input nodes is the identity function, the summed input to a McCulloch-Pitts neuron is nw-mp. Recall that the architecture mandates that one or more inhibitory inputs must cause the activation of the node to be zero. Using this information, we can derive an expression for the threshold.
![]()
As was mentioned earlier, there is no training algorithm for a McCulloch-Pitts neuron. As a result, all the weights and the threshold must be set manually. The threshold can be set using the expression derived above, and for simple networks the weights can be deduced fairly simply. In spite of this, it is clear to see that a McCulloch-Pitts neuron serves little use. The major reason for studying this network architecture is to become familiar with the operation of basic networks, understand the effects of the activation function and weights, and to understand later architectures which are based on the McCulloch-Pitts neuron .
![]()
Home Page ![]() Introduction
Introduction ![]() Biological Neural
Networks
Biological Neural
Networks ![]() McCulloch-Pitts Neuron
McCulloch-Pitts Neuron
Perceptron ![]() Adaline
Adaline ![]() Back Propagation
network
Back Propagation
network
References ![]() Research Paper
Research Paper ![]() Glossary
Glossary
![]() Beware: This
page is always under construction
Beware: This
page is always under construction
![]() Geocities
Geocities
![]() Geocities
Research Triangle
Geocities
Research Triangle